La moltiplicazione di un vettore per uno scalare
In questa lezione ti spiego cos'è e come si calcola il prodotto di un vettore per uno scalare.
Il prodotto del vettore per uno scalare è la moltiplicazione tra un vettore e un numero reale scalare qualsiasi. $$ \lambda \cdot \vec{v} $$
La variabile lambda è un numero reale qualsiasi.
Ad esempio, considera lambda uguale a due.
$$ \lambda = 2 $$
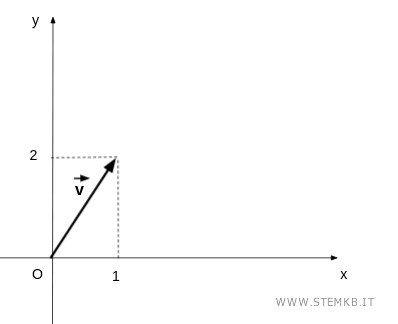
Ora prendi un vettore con componenti x=1 e y=2.
$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$
Sul piano il vettore si presenta in questo modo
Per calcolare il prodotto del vettore per lo scalare moltiplica ogni componente del vettore per lo scalare
$$ \lambda \cdot \vec{v} = 2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$
$$ \lambda \cdot \vec{v} = \begin{pmatrix} 2 \cdot 1 \\ 2 \cdot 2 \end{pmatrix} $$
il risultato che ottieni è il prodotto del vettore per lo scalare lambda=2
$$ \lambda \cdot \vec{v} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
Il prodotto del vettore per uno scalare è un altro vettore.
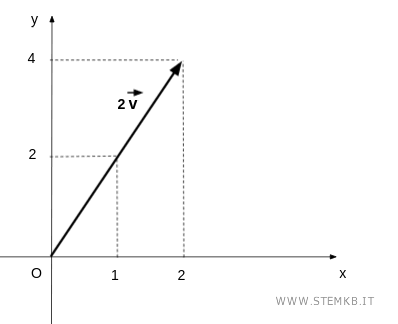
Il modulo (lunghezza) del vettore prodotto è uguale al prodotto tra il valore assoluto di lambda e il modulo del vettore iniziale.
In questo caso, la lunghezza del vettore prodotto è due volte quella del vettore iniziale.
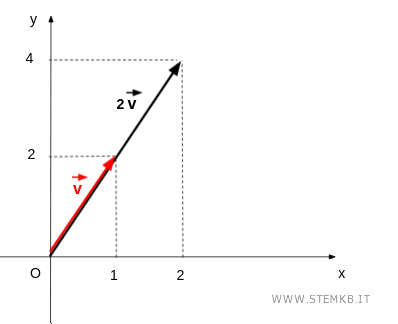
La direzione del vettore prodotto è la stessa perché il vettore si trova sulla stessa retta del vettore iniziale.
Il verso del vettore prodotto, invece, dipende dal segno dello scalare lambda.
- Se moltiplichi il vettore per un numero positivo (λ>0), il verso resta lo stesso.
- Se moltiplichi il vettore per un numero negativo (λ<0) il verso si inverte.
Per spiegarti meglio questo concetto ti faccio un altro esempio.
Moltiplica il vettore per lo scalare negativo lambda = -2
$$ \lambda \cdot \vec{v} = -2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} -2 \cdot 1 \\ -2 \cdot 2 \end{pmatrix} = \begin{pmatrix} -2 \\ -4 \end{pmatrix} $$
Il risultato è un vettore con la lunghezza (modulo) raddoppiata che la stessa direzione ma verso opposto rispetto al vettore iniziale.
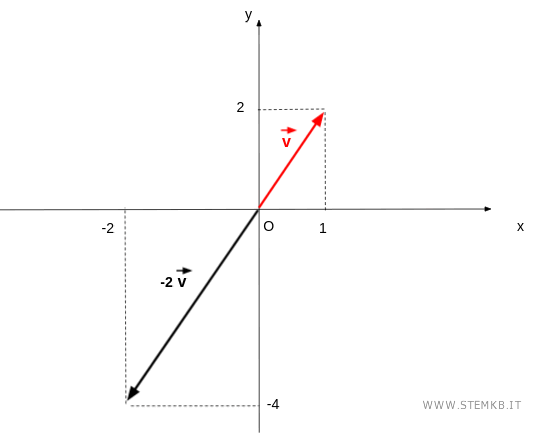
Nota. Se moltiplichi il vettore per lo scalare lambda = -1 ottieni il suo vettore opposto, ossia un vettore che ha la stessa direzione e modulo del vettore iniziale ma verso opposto.
Se questa lezione di StemKB ti piace, continua a seguirci.

