Il prodotto vettoriale
Il prodotto vettoriale è la moltiplicazione tra due vettori uxv che produce come risultato un vettore prodotto w $$ \vec{u} \ x \ \vec{v} = \vec{w} $$
Come si disegna il prodotto vettoriale
Per spiegarlo ti faccio un esempio pratico.
Traccia due vettori sul piano con Geogebra.
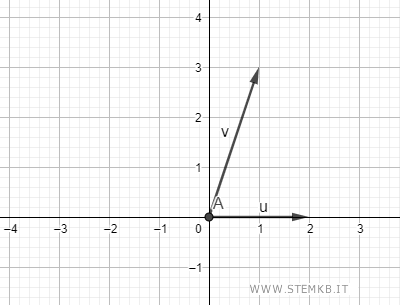
Il prodotto vettoriale è un vettore con una direzione perpendicolare al piano individuato dai vettori u e v.
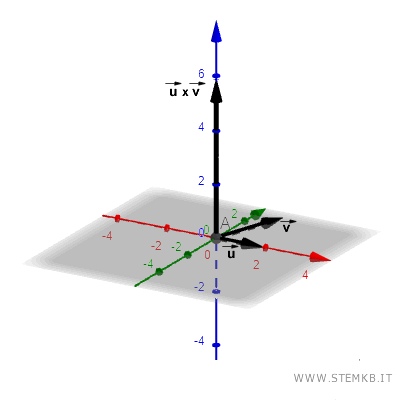
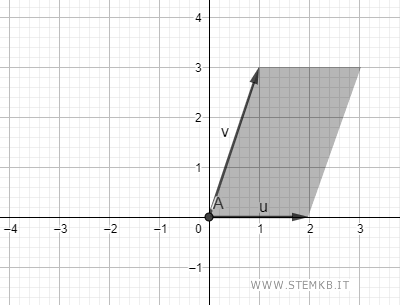
Il modulo del prodotto vettoriale u x v è uguale all'area del parallelogramma ottenuto usando i vettori u e v come lati.
In questo esempio l'area del parallelogramma è uguale a 6.
E in effetti il modulo (lunghezza) del vettore del prodotto vettoriale è lungo 6.
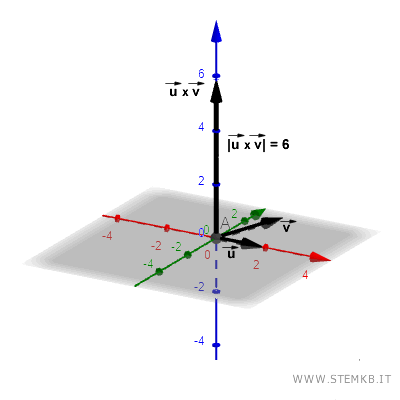
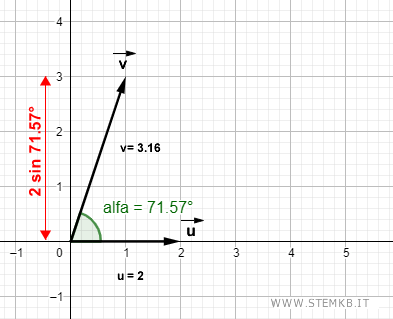
Il modulo del prodotto vettoriale è anche uguale al prodotto dei moduli dei vettori |u|·|v| per il seno dell'angolo tra i vettori a e b.
$$ |u \ x \ v| = |u| \cdot |v| \cdot \sin \alpha_{uv} $$
Dove |v|·sin αuv è la proiezione del secondo vettore.
Il verso del prodotto vettoriale lo ottieni usando il metodo della mano destra.
Sovrapponi il pollice della tua mano destra sul primo vettore (u) e l'indice sul secondo vettore (v) del prodotto vettoriale. Poi piega il medio.
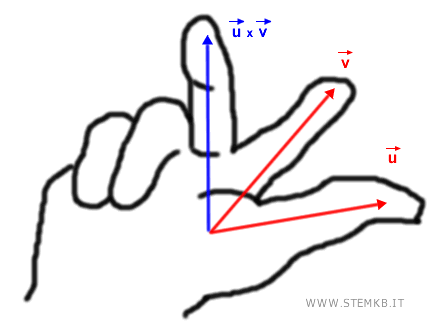
Il medio ti indica il verso del prodotto vettoriale.
Se hai disegnato i vettori alla lavagna, a seconda dei casi il medio è verso di te o verso il muro.
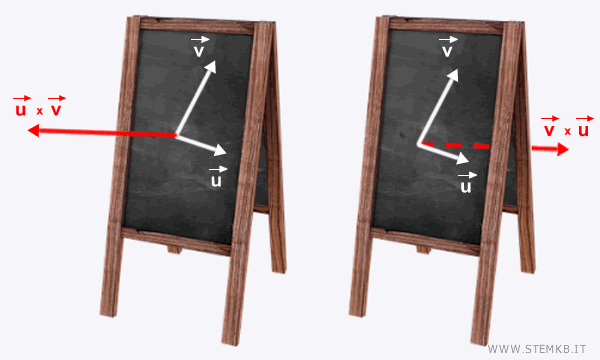
Nel primo caso il prodotto vettoriale esce dal foglio verso di te, mentre nel secondo caso entra nel muro.
Fai attenzione alla differenza. Nel primo caso il prodotto vettoriale è u x v, mentre nel secondo caso è v x u. Il pollice va messo sempre sul primo vettore del prodotto vettoriale. Quindi, nella lavagna a sinistra il pollice va messo sul vettore u mentre nella lavagna a destra il pollice va messo sul vettore v.

