Come calcolare la lunghezza del vettore

In questa lezione ti spiego come si calcola la lunghezza di un vettore tramite il teorema di Pitagora o il prodotto scalare del vettore per se stesso.

Ti faccio un esempio pratico.

Considera un vettore qualsiasi sul piano.

$$ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} $$

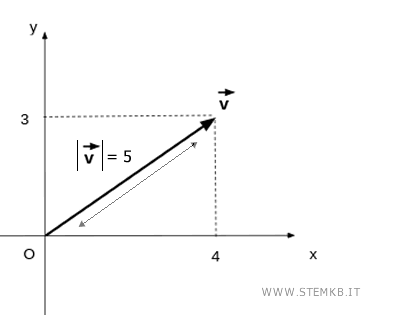
Le componenti x e y del vettore sono le coordinate (x,y) del vettore sul piano cartesiano.

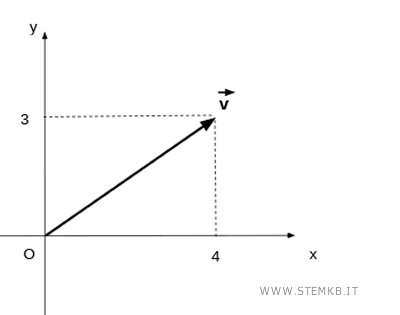
Il vettore forma un triangolo rispetto agli assi.

I segmenti sugli assi x=4 e y=3 sono i cateti del triangolo mentre la lunghezza del vettore |v| è l'ipotenusa.

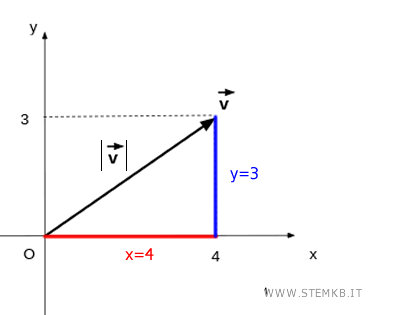
Secondo il teorema di Pitagora l'ipotenusa è la radice quadrata della somma dei quadrati dei cateti.

$$ ipotenusa = \sqrt{cateto_A^2+cateto_B^2} $$

Quindi, puoi applicare il teorema di Pitagora per calcolare la lunghezza del vettore.

In questo caso il cateto A è x=4, il cateto B è y=3 mentre l'ipotenusa è il modulo del vettore |v|.

$$ | \vec{v} | = \sqrt{x^2 + y^2}$$

Sostituisci x=3 e y=4

$$ | \vec{v} | = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 $$

Hai trovato la lunghezza del vettore.

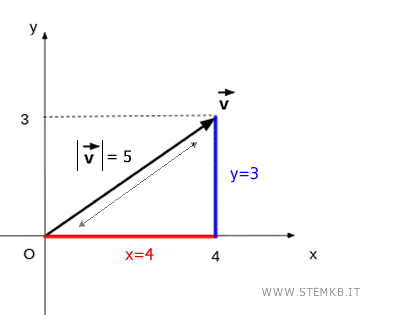
Nota. In algebra lineare la lunghezza del vettore si chiama anche modulo |v| o norma ||v||.

Un metodo alternativo

Puoi ottenere la lunghezza del vettore anche tramite il prodotto scalare del vettore per se stesso.

$$ \vec{v} \cdot \vec{v} = x \cdot x + y \cdot y = x^2 +y^2 $$

Come puoi vedere il prodotto scalare del vettore per se stesso è uguale alla somma dei quadrati x²+y²

Secondo il teorema di Pitagora la somma dei quadrati è il modulo del vettore al quadrato |v|²=x²+y²

Sostituisci x=3 e y=4

$$ \vec{v} \cdot \vec{v} = 3^2 +4^2 = 9 + 16 = 25 $$

Calcola la radice quadrata del prodotto scalare del vettore per se stesso.

$$ \sqrt{ \vec{v} \cdot \vec{v} } = \sqrt{25} = 5 $$

Il risultato finale è il modulo del vettore ossia la lunghezza del vettore.

Se questa lezione di StemKB ti piace continua a seguirci.