Le operazioni tra vettori

L'algebra vettoriale è un ramo della matematica che tratta le operazioni, come la somma, la sottrazione e la moltiplicazione, su grandezze fisiche che hanno sia una magnitudine sia una direzione, conosciute come vettori.

Le grandezze vettoriali non si limitano a un semplice valore, ma includono anche una direzione e un verso. Di conseguenza, non puoi gestirle come numeri normali utilizzando le regole standard dell'algebra.

Per i vettori, devi utilizzare un tipo speciale di matematica, chiamata algebra vettoriale, che stabilisce come eseguire le operazioni tra vettori.

Le operazioni dell'algebra vettoriale

Ci sono due operazioni fondamentali che si possono fare tra vettori: l'addizione (o sottrazione) e il prodotto.

• Addizione di vettori
  Quando sommi due vettori, stai unendo le due direzioni dei vettori. Immagina di camminare 10 passi verso nord da A a B (questo è un vettore) e poi 5 passi verso est da B a C.
  
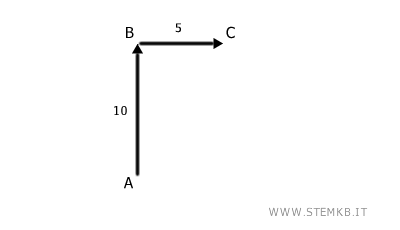
  La somma di questi due vettori è il percorso totale che hai percorso, ossia il vettore da A a C. In questo caso è un percorso diagonale. Quindi, il risultato finale della somma di due vettori è un altro vettore.
  
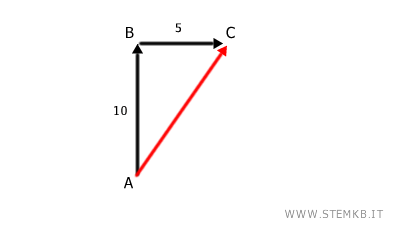
  In termini matematici, l'addizione di vettori si esegue sommando le componenti corrispondenti dei vettori. Per esempio, se hai due vettori $$ \vec{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} $$ $$ \vec{b} = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} $$ il vettore somma S è la somma delle rispettive componenti $$ \vec{a} + \vec{b} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} + \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} = \begin{pmatrix} a_1 + b_1 \\ a_2 + b_2 \end{pmatrix} $$
• La moltiplicazione tra vettori
  Nell'algebra vettoriale ci sono due tipi principali di prodotti tra vettori, il prodotto scalare e il prodotto vettoriale.
  • Prodotto Scalare (o Prodotto Interno)
    Quando moltiplichi due vettori con il prodotto scalare, ottieni come risultato un numero scalare, ossia un numero e non un altro vettore. Per calcolare il prodotto scalare di due vettori, devi moltiplicare le componenti corrispondenti dei vettori e poi sommare i risultati. Ad esempio, se hai due vettori $$ \vec{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} $$ $$ \vec{b} = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} $$ il prodotto scalare P è uguale alla somma dei prodotti tra le corrispondenti componenti dei due vettori $$ P = a_1 \cdot b_1 + a_2 \cdot b_2 $$ Il prodotto scalare è legato all'angolo tra i vettori. Se i due vettori sono ortogonali, ossia se l'angolo tra loro è 90 gradi, il prodotto scalare è zero.
  • Prodotto Vettoriale (o Prodotto Esterno)
    Quando moltiplichi due vettori con il prodotto vettoriale, ottieni un nuovo vettore come risultato. Il prodotto vettoriale di due vettori ha una magnitudine (o lunghezza) che è proporzionale al prodotto delle lunghezze dei vettori e al seno dell'angolo tra di essi, e una direzione perpendicolare al piano contenente i due vettori originali (determinata dalla regola della mano destra). Questo prodotto si applica principalmente a vettori nello spazio tridimensionale.

Ricorda, le operazioni tra vettori non seguono sempre le stesse regole delle operazioni con numeri scalari. Ad esempio, il prodotto di due vettori non è commutativo, cioè cambiare l'ordine dei vettori nel prodotto vettoriale cambia il segno del risultato.