Come calcolare l'angolo tra due vettori

In questa lezione ti spiego come si calcola l'angolo α compreso tra due vettori v₁ e v₂ tramite questa formula $$ \alpha = \arccos ( \frac{ \vec{v_1} \cdot \vec{v_2} }{|\vec{v_1} | \cdot |\vec{v_2} | } ) $$

Ti faccio un esempio pratico

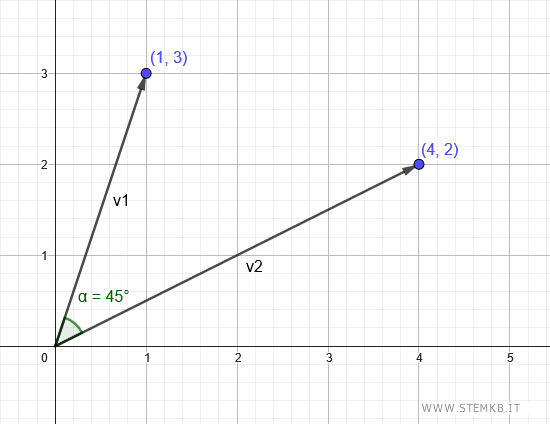
Considera due vettori v₁ e v₂

$$ \vec{v_1} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} $$

$$ \vec{v_2} = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$

Le componenti x e y dei vettori corrispondono alle coordinate (x,y) dei vettori sul piano cartesiano.

I due vettori v₁ e v₂ formano un angolo di ampiezza α che ancora non conosciamo.

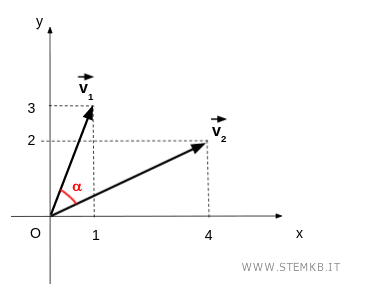
Come si calcola l'angolo tra i vettori?

Il prodotto scalare dei due vettori è uguale al prodotto dei moduli (lunghezze) dei due vettori per il coseno dell'angolo α compreso tra i due vettori.

$$ \vec{v_1} \cdot \vec{v_2} = |\vec{v_1} | \cdot |\vec{v_2} | \cdot \cos \alpha $$

Metti in evidenza il coseno dell'angolo alfa

$$ \cos \alpha = \frac{ \vec{v_1} \cdot \vec{v_2} }{|\vec{v_1} | \cdot |\vec{v_2} | } $$

Poi calcola l'arcocoseno in entrambi i membri dell'equazione

$$ \arccos( \cdot \cos \alpha ) = \arccos ( \frac{ \vec{v_1} \cdot \vec{v_2} }{|\vec{v_1} | \cdot |\vec{v_2} | } ) $$

L'arcocoseno del coseno di alfa è l'angolo alfa

$$ \alpha = \arccos ( \frac{ \vec{v_1} \cdot \vec{v_2} }{|\vec{v_1} | \cdot |\vec{v_2} | } ) $$

Quindi, l'angolo alfa è uguale al rapporto tra il prodotto scalare dei vettori per il prodotto dei moduli dei vettori.

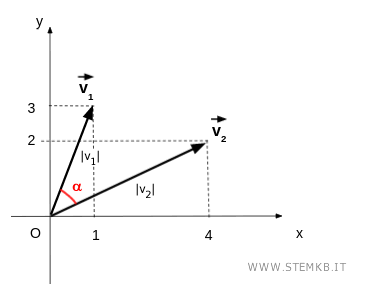
Ora calcola i moduli dei due vettori usando il teorema di Pitagora

$$ | \vec{v_1} | = \sqrt{3^2 +1^2 } = \sqrt{10} $$

$$ | \vec{v_2} | = \sqrt{4^2 +2^2 } = \sqrt{20} $$

I moduli |v₁| e |v₂| sono le lunghezze dei due vettori.

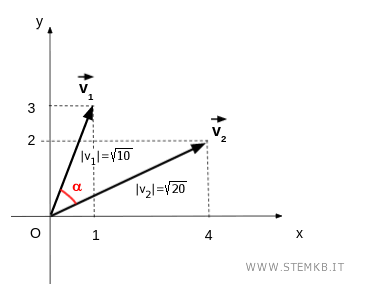
Sostituisci i moduli dei vettori |v₁| = √10 e |v₂| = √20 nella formula precedente

$$ \alpha = \arccos ( \frac{ \vec{v_1} \cdot \vec{v_2} }{|\vec{v_1} | \cdot |\vec{v_2} | } ) $$

$$ \alpha = \arccos ( \frac{ \vec{v_1} \cdot \vec{v_2} }{\sqrt{10} \cdot \sqrt{20} } ) $$

$$ \alpha = \arccos ( \frac{ \vec{v_1} \cdot \vec{v_2} }{\sqrt{200} } ) $$

Ora calcola il prodotto scalare dei due vettori

$$ \vec{v_1} \cdot \vec{v_2} = x_1 \cdot x_2 + y_1 \cdot y_2 = 1 \cdot 4 + 3 \cdot 2 = 4+6=10 $$

Sostituisci il prodotto scalare v₁·v₂ = 10 nella formula precedente

$$ \alpha = \arccos ( \frac{ \vec{v_1} \cdot \vec{v_2} }{\sqrt{200} } ) $$

$$ \alpha = \arccos ( \frac{ 10 }{\sqrt{200} } ) $$

$$ \alpha = \arccos ( 0.71 ) $$

A questo punto calcola l'arcocoseno di 0.71

$$ \alpha = \arccos ( 0.71 ) = 45° $$

$$ \alpha = 45° $$

Il risultato finale α = 45° è l'ampiezza dell'angolo tra i due vettori

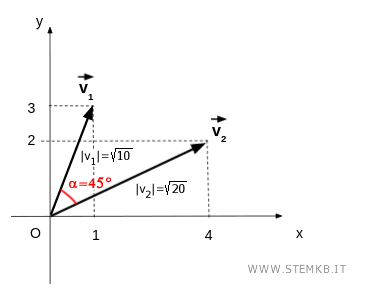
Verifica. Per verificare il risultato appena calcolato puoi usare Geogebra. Crea due vettori con le coordinate dell'esempio precedente e calcola l'angolo tra i due vettori.

Se questa lezione di algebra lineare di StemKB ti piace continua a seguirci.