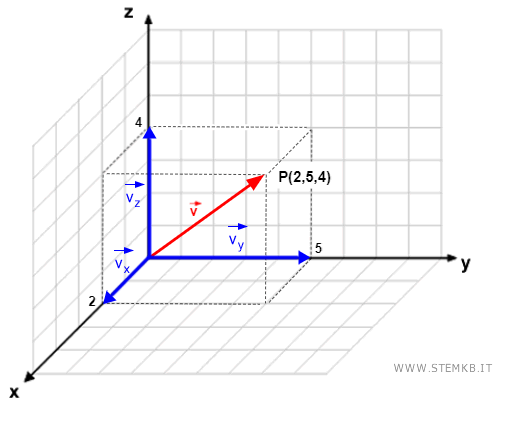
La scomposizione cartesiana di un vettore

La scomposizione cartesiana di un vettore consiste nel dividere un vettore in componenti lungo gli assi del sistema di coordinate cartesiane. $$ \vec{v} = x \cdot \vec{u}_x + y \cdot \vec{u}_y + z \cdot \vec{u}_z $$

Quando rappresentiamo un vettore in un piano cartesiano, possiamo scomporlo nelle sue componenti cartesiane, ossia due valori numerici che indicano le proiezioni del vettore sugli assi \(x\) e \(y\).

Questo processo di scomposizione è fondamentale in fisica e matematica per analizzare i vettori in termini di coordinate.

E' particolarmente utile quando si lavora in due o tre dimensioni.

Ecco un esempio pratico.

Supponi di avere un vettore v (4;5) in uno spazio a due dimensioni.

$$ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 4 \\ 5 \end{pmatrix} $$

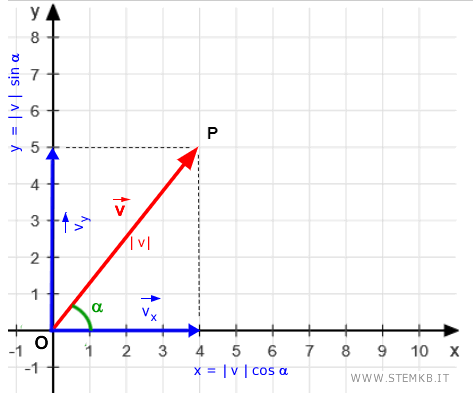
Il primo estremo del vettore ha origine nel punto (0;0) mentre il secondo estremo giunge alle coordinate (x;y)=(4;5).

Puoi rappresentare il vettore v sul piano cartesiano.

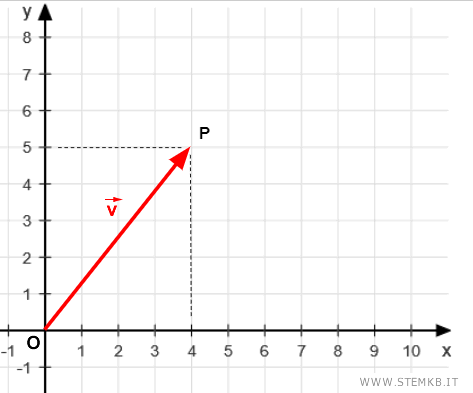
Ora proietta il secondo estremo del vettore sugli assi cartesiani.

In questo modo hai ottenuto altri due vettori: un vettore v_x sull'asse x e un vettore v_y sull'asse y.

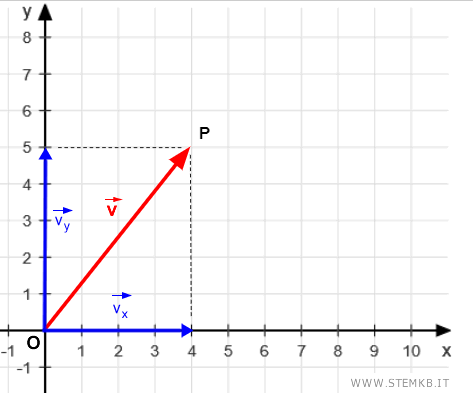
Come puoi facilmente notare, la somma di questi due vettori v_x+v_y è uguale al vettore iniziale v.

Puoi verificarlo usando il metodo del parallelogramma o il metodo punta-coda.

$$ \vec{v} = \vec{v}_x + \vec{v}_y $$

Quindi, puoi scrivere il vettore iniziale v come la somma delle sue componenti.

Sapendo che i vettori v_x=4·u_x e v_y=5·u_y, puoi scrivere la somma anche in questo modo:

$$ \vec{v} = 4 \cdot \vec{u}_x + 5 \cdot \vec{u}_y $$

Dove u_x e u_y sono i versori ossia i vettori di lunghezza unitaria degli assi cartesiani.

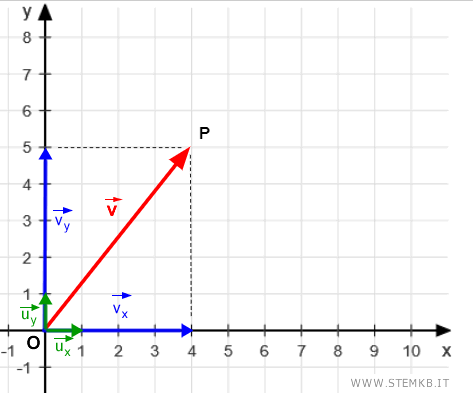
In generale, la scomposizione di qualsiasi vettore si presenta in questo modo

$$ \vec{v} = x \cdot \vec{u}_x + y \cdot \vec{u}_y $$

Dove "x" e "y" sono le coordinate del vettore iniziale v, ossia i moduli (lunghezze) dei vettori v_x e v_y che hai proiettato sugli assi cartesiani.

Come trovare le componenti del vettore

Puoi ottenere i valori di "x" e "y" anche usando un po' di trigonometria, se conosci il modulo (lunghezza) del vettore, indicato con $ | \vec{v} | $, e l’angolo \(\alpha\) che il vettore forma con l'asse \(x\) misurato in senso antiorario.

$$ x = | \vec{v} | \cdot \cos \alpha = 4 $$

$$ y = | \vec{v} | \cdot \sin \alpha = 5 $$

Dove |v| è il modulo (lunghezza) del vettorie iniziale v mentre alfa è l'angolo del vettore iniziale rispetto al semiasse positivo delle ascisse.

Queste ultime due identità trigonometriche sono molto utili in fisica.

Quindi, ti consiglio di tenerle bene a mente.

Facciamo un esempio pratico.

Supponiamo di avere un vettore con modulo \( | \vec{v} | = 10\) unità e un angolo \(\alpha = 30^\circ\).

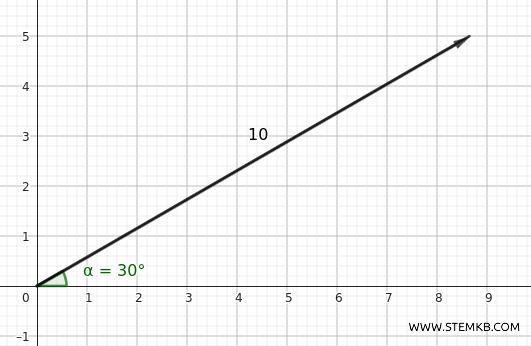
La sua componente \(x\) sarà approssimativamente 8.66.

$$ x = 10 \cdot \cos 30^\circ = 10 \cdot \frac{\sqrt{3}}{2} \approx 8.66 $$

La componente \(y\) sarà 5

$$ t = 10 \cdot \sin 30^\circ = 10 \cdot \frac{1}{2} = 5 $$

Quindi, il vettore ha le coordinate cartesiane \( (8.66, 5) \).

Allo stesso modo puoi scomporre un vettore in uno spazio tridimensionale. $$ \vec{v} = x \cdot \vec{u}_x + y \cdot \vec{u}_y + z \cdot \vec{u}_z $$ In questo caso la scomposizione cartesiana sarà data da tre componenti (v_x, v_y, v_z) ossia vettori che rappresentano rispettivamente le proiezioni del vettore lungo l'asse x, l'asse y e l'asse z.