Il gruppo speciale ortogonale reale

Il gruppo speciale ortogonale reale $ SO(n, \mathbb{R}) $ comprende tutte le matrici quadrate di ordine $ n $ con elementi reali che sono al contempo ortogonali e con determinante pari a uno.

L'ortogonalità di una matrice $ A $ si riferisce alla condizione $ A^TA = I $, ovvero il prodotto della matrice per la sua trasposta restituisce la matrice identità $ I $.

La condizione sul determinante $ \det(A) = 1 $, invece, assicura che la trasformazione preservi l'orientazione dello spazio.

In pratica, questo gruppo rappresenta l'insieme dei movimenti rigidi nello spazio $ \mathbb{R}^n $ che mantengono l'orientazione originale degli oggetti e lasciano invariata la posizione dell'origine.

Preservazione dell'orientazione
Significa che questi movimenti non capovolgono l'oggetto; l'orientamento iniziale viene mantenuto.
Per esempio, una figura non viene specchiata o rovesciata durante la trasformazione.
Lasciare fissa l'origine
Vuol dire che questi movimenti non spostano il punto di origine dello spazio Rⁿ; quindi, se applichiamo il movimento a tutto lo spazio, l'origine rimarrà dove è.
Ad esempio, il gruppo speciale ortogonale reale consiste in tutte le rotazioni attorno all'origine nello spazio a n dimensioni che non capovolgono l'oggetto.

In altre parole, dopo un movimento rigido, la forma e la dimensione di un oggetto rimangono invariate, anche se la sua posizione nello spazio potrebbe cambiare.

Questi movimenti sono cruciali in molte applicazioni perché permettono di manipolare oggetti nello spazio senza alterarne la forma o il volume.

Esempio

Consideriamo la matrice seguente:

$$ A = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} $$

E' un esempio specifico di una matrice 2x2 in $ SO(2, \mathbb{R}) $ perché soddisfa tutte le condizioni del gruppo speciale ortogonale reale.

E' una matrice quadrata. Il numero di righe è uguale al numero delle colonne.
Il determinante della matrice è uguale a 1 $$ \det(A) = 0 \cdot 0 - (-1) \cdot 1 = 1 $$
E' una matrice ortogonale perché il prodotto della matrice A con la sua matrice inversa A-1 è uguale alla matrice identità. $$ AA^{-1} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = I $$

Questa matrice rappresenta una rotazione di 90 gradi (o $ \frac{\pi}{2} $ radianti) in senso antiorario attorno all'origine del piano cartesiano.

Se applichiamo questa matrice a un punto, diciamo $ (x, y) $, otteniamo le nuove coordinate del punto dopo la rotazione.

Ad esempio, applichiamo la matrice al punto $ P(1, 0) $:

\[
\begin{pmatrix}
0 & -1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
1 \\
0
\end{pmatrix}
=
\begin{pmatrix}
0 \cdot 1 + (-1) \cdot 0 \\
1 \cdot 1 + 0 \cdot 0
\end{pmatrix}
=
\begin{pmatrix}
0 \\
1
\end{pmatrix}
\]

Il punto $ P(1, 0) $, dopo la rotazione di 90 gradi antiorario, si sposta in P' $ (0, 1) $, che è esattamente a 90 gradi da dove ha iniziato nel sistema di coordinate standard del piano.

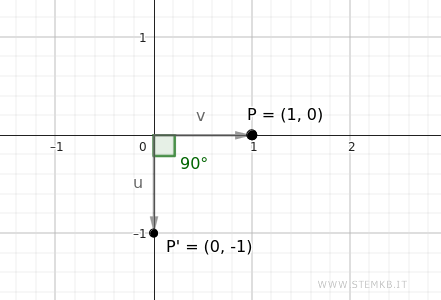
il punto si sposta di 90°

Il vettore $ \mathbf{v} $ che indica la posizione del punto $ P $ ruota di 90 gradi, trasformandosi nel vettore $ \mathbf{u} $, che ora punta verso la nuova posizione $ P' $.