Ordine di un elemento in un gruppo

L'ordine di un elemento $ g $ in un gruppo $ (G, \cdot) $, indicato spesso con $ |g| $, è il più piccolo intero positivo $ r $ per il quale la potenza dell'elemento $ g^r $ è uguale all'elemento neutro $ e $ del gruppo $$ g^r = e $$

Se questo numero intero positivo $ r $ esiste, diremo che l'elemento $ g $ ha un ordine n (o periodo n).

Se invece non esiste, cioè se non importa quante volte applichiamo l'operazione del gruppo all'elemento $ g $, non otterremo mai l'elemento neutro, allora diciamo che $ g $ ha ordine infinito.

Quest'ultima situazione si verifica in genere nei gruppi infiniti, come $ (Z, +) $, il gruppo degli interi con l'operazione di addizione.

In termini più pratici, se consideriamo un gruppo finito come $ (Z_n, +) $, l'ordine di un elemento corrisponde al numero di volte che dobbiamo sommare quell'elemento con se stesso per ottenere un risultato che è congruo a zero modulo $ n $, che è l'elemento neutro nel contesto dell'addizione modulo $ n $.

Esempi
Ordine infinito di un elemento
Ordine finito di un elemento

Esempi

Ecco alcuni esempi per chiarire il concetto:

Nel gruppo $ (Z_4, +) $, dove $ Z_4 $ rappresenta le classi di resto modulo $ 4 $, l'elemento $ 1 $ ha ordine $ 4 $ perché $ 1+1+1+1 = 4 \equiv 0 $ modulo $ 4 $.

Significa che sommando $ 1 $ a se stesso quattro volte, si ottiene $ 0 $, l'elemento neutro del gruppo.

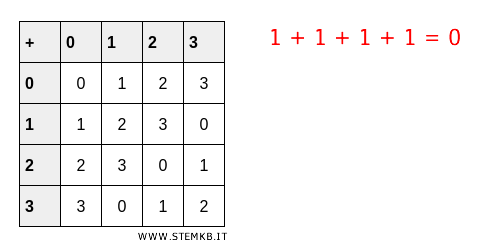
example

Esempio 2

Sempre in $ (Z_4, +) $, l'elemento $ 2 $ ha ordine $ 2 $ poiché $ 2+2 = 4 \equiv 0 $ modulo $ 4 $.

Solo due somme sono necessarie per ritornare allo zero, che è l'elemento neutro.

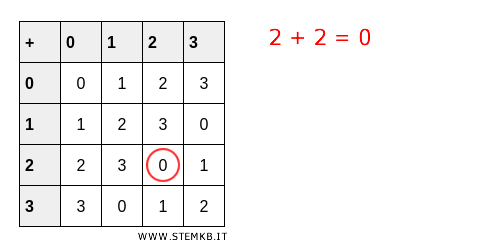
esempio

Esempio 3

Calcoliamo l'ordine dell'elemento $ 3 $ in $ Z_4 $:

$$ 3 + 3 \equiv 6 \equiv 2 \mod 4 $$

$$ 3 + 3 + 3 \equiv 9 \equiv 1 \mod 4 $$

$$ 3 + 3 + 3 + 3 \equiv 12 \equiv 0 \mod 4 $$

La prima somma non dà 0 modulo 4, e nemmeno la seconda.

Tuttavia, la terza somma, che equivale a sommare $ 3 $ quattro volte, dà un risultato di 0 modulo 4.

Questo significa che $ 3 $ ha ordine 4 in $ Z_4 $ perché $ 4 $ è il più piccolo intero positivo che moltiplicato per $ 3 $ dà un risultato che è un multiplo di $ 4 $, che è lo stesso di dire che è congruente a 0 modulo 4

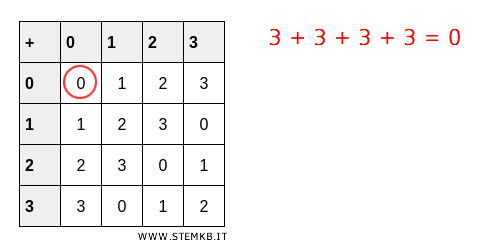
esempio

Esempio 4

L'elemento neutro di qualsiasi gruppo ha sempre ordine $ 1 $, perché qualsiasi elemento neutro, per definizione, soddisfa la proprietà $ e = e $.

Ad esempio, nel gruppo (Z_4, +) \) modulo 4 lo zero è già l'elemento neutro del gruppo.

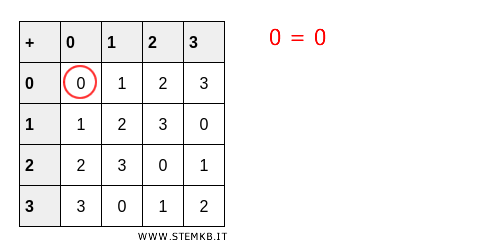
lo zero ha ordine uno

Esempio 5

Per $ (Z, +) $, che è il gruppo di tutti gli interi sotto l'operazione di addizione, ogni elemento $ a \neq 0 $ ha ordine infinito.

Questo accade perché se non partiamo da $ 0 $, non importa quante volte aggiungiamo $ a $ a se stesso, non arriveremo mai all'elemento neutro $ 0 $.

L'ordine di un elemento in un gruppo è un concetto fondamentale in algebra astratta e nella teoria dei gruppi, poiché ha implicazioni dirette sulle strutture dei gruppi e sulle loro proprietà, come la ciclicità di un gruppo o la possibilità di costruire sottogruppi generati da singoli elementi.

Ordine infinito di un elemento

Se un elemento $ g $ di un gruppo $ G $ ha un ordine (o periodo) infinito, significa che per ogni intero positivo $ n $, l'elemento $ g^n $ non è mai uguale all'elemento neutro del gruppo $ e $. Ad eccezione del caso $ g^0 = e $ che vale per definizione in qualsiasi gruppo.

Quindi, se prendiamo due interi $ s $ e $ t $ tali che $ s \neq t $, allora $ g^s $ e $ g^t $ sono due elementi distinti del gruppo $ G $.

Questo accade perché, dato che $ g $ ha ordine infinito, non ci sono due potenze distinte che portano al medesimo risultato.

Esempio

Per esempio, consideriamo il gruppo additivo $ \mathbb{Z} $, che è l'insieme di tutti gli interi sotto l'operazione di addizione.

L'elemento neutro in questo gruppo è $ 0 $, e ogni elemento (ogni intero) ha ordine infinito: per nessun intero $ n $ diverso da zero avremo che $ n $ sommato a se stesso un certo numero finito di volte darà $ 0 $.

Se prendiamo $ g = 1 $ in $ \mathbb{Z} $, possiamo vedere che $ g^s = s $ e $ g^t = t $ per due interi distinti $ s $ e $ t $ saranno sempre diversi, perché $ s $ e $ t $ sono diversi numeri interi.

Il sottogruppo ciclico generato da $ g $, che in questo caso è $ \langle g \rangle = \{ ..., -3, -2, -1, 0, 1, 2, 3, ... \} $, è chiaramente infinito, poiché contiene un numero infinito di elementi.

Questo esempio mostra come un elemento con ordine infinito in un gruppo $ G $ porta alla formazione di un sottogruppo ciclico infinito $ \langle g \rangle $.

Ordine finito di un elemento

Se un elemento $ g $ in un gruppo $ G $ ha periodo finito $ n $, allora questo elemento $ g $ dà origine a un sottogruppo ciclico $ \langle g \rangle $ avente $ n $ come numero totale di elementi distinti.

La rappresentazione di tale sottogruppo è data da $ \langle g \rangle = \{ e, g, g^2, \ldots, g^{n-1} \} $, dove $ e $ è l'elemento neutro del gruppo, identificabile anche con $ g^0 $.

Per ogni coppia di interi $ s $ e $ t $, gli elementi $ g^s $ e $ g^t $ saranno identici se e soltanto se $ s $ e $ t $ sono congruenti modulo $ n $, cioè se $ s $ è uguale a $ t $ più un multiplo di $ n $.

Esempio

Consideriamo il gruppo delle rotazioni di un cerchio, dove ogni rotazione è determinata da un angolo e l'operazione del gruppo è la composizione delle rotazioni.

Il gruppo è denotato da $ G $ e l'elemento neutro è la rotazione di 0 gradi, che corrisponde all'identità (nessuna rotazione).

Sia $ g $ un elemento di $ G $ che rappresenta una rotazione di 60 gradi. Il periodo di $ g $ è $ n = 6 $ perché dopo sei rotazioni di 60 gradi ritorniamo alla posizione iniziale: $ g^6 = e $, dove $ e $ è l'elemento neutro.

Il sottogruppo ciclico generato da $ g $, denotato $ <g> $, consiste di tutti gli elementi che possono essere rappresentati come potenze di $ g $:

$$ <g> = \{ g^0, g^1, g^2, g^3, g^4, g^5 \} $$

Dove:
$ g^0 = e $ (la rotazione di 0 gradi)
$ g^1 $ è una rotazione di 60 gradi
$ g^2 $ è una rotazione di 120 gradi
$ g^3 $ è una rotazione di 180 gradi
$ g^4 $ è una rotazione di 240 gradi
$ g^5 $ è una rotazione di 300 gradi

Il sottogruppo $ <g> $ ha cardinalità $ n = 6 $, il che significa che contiene sei elementi distinti.

Ora, per quanto riguarda l'uguaglianza delle potenze, se prendiamo due numeri interi $ s $ e $ t $ tali che $ g^s = g^t $, questo sarà vero se e solo se $ s $ è congruente a $ t $ modulo $ n $.

Per esempio, se $ s = 8 $ e $ t = 2 $, abbiamo che $ g^8 = g^2 $ perché $ 8 $ è congruente a $ 2 $ modulo $ 6 $ (cioè, $ 8 $ differisce da $ 2 $ per un multiplo di $ 6 $).

In termini di rotazioni, questo significa che una rotazione di 480 gradi (equivalente a $ g^8 $) porta nella stessa posizione di una rotazione di 120 gradi (equivalente a $ g^2 $), poiché entrambe le rotazioni sono separabili da multipli completi di 360 gradi, che corrispondono a una rotazione completa e quindi non alterano la posizione finale.