
Numeri opposti
I numeri opposti sono coppie di numeri che, se sommati, danno come risultato zero. $$ a + (-a) = 0 $$
In altre parole, ogni numero ha un numero opposto che è identico in valore assoluto, ma ha il segno invertito.
Sono anche detti inversi additivi.
Per esempio, il numero opposto di \(5\) è \(-5\), e viceversa. Questo perché \(5 + (-5) = 0\).
$$ 5 + (-5) = 0 $$
Analogamente, l’opposto di \(-3\) è \(3\), poiché \(-3 + 3 = 0\).
$$ 3 + (-3) = 0 $$
Immagina di trovarti su una linea retta, come quella dei numeri che hai visto a scuola: a sinistra ci sono i numeri negativi, al centro c’è lo zero e a destra i numeri positivi.
Ogni numero sulla linea ha un "numero opposto" che si trova alla stessa distanza dallo zero, ma nella direzione opposta.
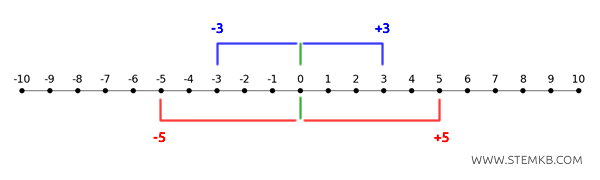
Questa idea, semplice e intuitiva, è alla base del concetto di "numeri opposti" in matematica.
Quando rappresenti i numeri interi su una retta, due numeri opposti sono punti simmetrici rispetto all'origine (lo zero).
Questa caratteristica è fondamentale non solo per capire meglio la simmetria dei numeri, ma anche per risolvere problemi pratici.
Pensiamo a situazioni concrete. Immagina di dover salire o scendere delle scale. Se pensi a ogni gradino salito come un numero positivo (+1, +2, +3), ogni gradino sceso sarà un numero negativo (-1, -2, -3). Se sali tre gradini e poi ne scendi tre, sei tornato al punto di partenza, esattamente come succede con \(3 + (-3) = 0\). Ecco un esempio di numeri opposti nella vita di tutti i giorni! Un altro esempio si trova nella finanza personale. Supponiamo che tu abbia \(10\) euro di credito sul tuo conto (lo rappresentiamo con \(+10\)) e poi debba pagare un debito di \(10\) euro. La somma delle due cifre, \(10 + (-10)\), ti riporta a zero, esattamente come succede con i numeri opposti.
Qual è il valore opposto di zero?
Lo zero è l'unico numero ad avere come numero opposto se stesso, perché non ha segno.
$$ -0 = 0 $$
Infatti, per definizione, il numero opposto di un numero \( x \) è il valore che, sommato ad \( x \), dà zero. Nel caso di zero, abbiamo:
$$ 0 + (-0) = 0 $$
Quindi lo zero soddisfa perfettamente questa proprietà, senza richiedere un cambiamento di segno.
Anche l’espressione \( -0 = 0 \) riflette questa particolarità: non ha senso parlare di "segno" per lo zero, poiché si trova esattamente al centro della linea dei numeri, in equilibrio perfetto tra positivi e negativi.
Questa unicità dello zero lo rende un elemento fondamentale in molti contesti matematici e algebrici, dove funziona come elemento neutro dell'addizione, o "identità additiva".
Il valore assoluto dei numeri
Per comprendere a fondo i numeri opposti, è utile parlare anche di valore assoluto. Il valore assoluto di un numero è la sua distanza dallo zero, senza considerare il segno.
Quindi, sia \(5\) che \(-5\) hanno un valore assoluto di \(5\).
$$ | 5 | = | - 5 | = 5 $$
Il valore assoluto ti mostra quanto “vale” un numero indipendentemente dalla sua direzione sulla linea dei numeri.
Questa misura è importante, per esempio, in fisica, dove la distanza è sempre positiva, anche se ci muoviamo in direzione opposta rispetto a un punto di partenza.
Ad esempio, per andare da Roma a Parigi in autostrada bisogna percorrere circa 1400 chilometri. Allo stesso modo, anche per il viaggio di ritorno da Parigi a Roma la distanza sarà sempre di 1400 chilometri. Le distanze, infatti, sono sempre espresse come valori positivi.
In definitiva, i numeri opposti ci ricordano l’importanza dell’equilibrio e della simmetria: per ogni movimento in una direzione, esiste sempre la possibilità di tornare indietro.
Quindi, comprendere i numeri opposti è anche il primo passo verso concetti matematici più complessi, come le equazioni e i vettori, e ti aiuta a vedere i numeri non solo come semplici entità isolate, ma come parti di un sistema coerente e bilanciato.

