Il massimo comune divisore

Il massimo comune divisore tra due o più numeri \(a\) e \(b\), diversi da zero, è definito come il numero più grande che divide ciascuno di essi senza lasciare resto. $$ M.C.D.(a, b) $$ E' il più grande tra i divisori comuni di \(a\) e \(b\).

Per capire meglio il concetto di massimo comune divisore (M.C.D.), possiamo partire da un esempio pratico.

Esempio

Dobbiamo trovare il massimo comune divisore dei numeri 36 e 60, cioè il più grande tra i divisori comuni tra questi due numeri.

Per prima cosa, elenchiamo tutti i numeri che dividono 36 senza lasciare resto. I divisori di 36 sono:

$$ 1, 2, 3, 4, 6, 9, 12, 18, 36 $$

Ora elenchiamo i divisori di 60, cioè i numeri che dividono 60 senza lasciare resto:

$$ 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 $$

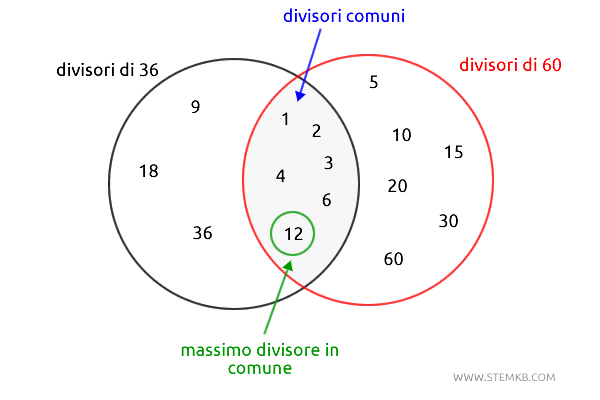
Per trovare i divisori comuni a 36 e 60, cerchiamo i numeri che si trovano in entrambe le liste:

$$ 1, 2, 3, 4, 6, 12 $$

Tra questi divisori comuni, il numero più grande è 12.

Questo significa che 12 è il massimo comune divisore di 36 e 60.

Quindi, possiamo quindi scrivere:

$$ M.C.D.(36, 60) = 12 $$

Sia 36 che 60 sono divisibili per 12 ed è il divisore più grande che questi due numeri hanno in comune.

Nel prossimo paragrafo vediamo altri metodi utili per calcolare il massimo comune divisore.

Metodi per calcolare il M.C.D.

Esistono anche altri metodi per trovare il massimo comune divisore, come:

• La scomposizione in fattori primi
  Si scompongono entrambi i numeri nei loro fattori primi e si moltiplicano solo i fattori comuni con l’esponente più basso.

  Esempio. Calcola il massimo comune divisore tra 36 e 60 usando il metodo della scomposizione in fattori primi. Scomponi 36 nei suoi fattori primi: $$ 36 = 2^2 \times 3^2 $$ Poi scomponi 60 nei suoi fattori primi: $$ 60 = 2^2 \times 3^1 \times 5^1 $$ Ora che hai la scomposizione in fattori primi di entrambi i numeri, per trovare il M.C.D., considera solo i fattori comuni a entrambi i numeri con l’esponente più basso ($ 2^2 $ e $ 3^1 $ ). Quindi, il prodotto dei fattori comuni con gli esponenti più bassi è: $$ M.C.D.(36, 60) = 2^2 \times 3^1 = 4 \times 3 = 12 $$ Hai trovato che il massimo comune divisore tra 36 e 60 è 12. E' lo stesso risultato già ottenuto in precedenza.

• L’algoritmo di Euclide
  E' un metodo efficiente che utilizza la divisione successiva per trovare il M.C.D. tra due numeri. Si basa su una serie di divisioni successive fino a ottenere un resto pari a zero. Quando ciò accade, l'ultimo divisore utilizzato è il massimo comune divisore. Questo algoritmo è particolarmente utile per numeri molto grandi. 

  Esempio. Prova ad applicare l'algoritmo di Euclide per trovare il massimo comune divisore di 36 e 60. Prendiamo i due numeri, 60 e 36, e dividi il più grande per il più piccolo: $$ 60 \div 36 = 1 \text{ con resto } 24 $$ Il resto è 24. Quindi, ripeti il procedimento, dividi il divisore 36 per il resto 24. $$ 36 \div 24 = 1 \text{ con resto } 12 $$ Il resto è 12. Ora dividi il divisore \( 24 \) per il resto \(12 \) $$ 24 \div 12 = 2 \text{ con resto } 0 $$ Questa volta, il resto è zero. Quando ottieni un resto uguale a zero, l'ultimo divisore non nullo (in questo caso, 12) è il massimo comune divisore tra i due numeri iniziali. Quindi, il massimo comune divisore tra 36 e 60, calcolato con l'algoritmo di Euclide, è: $$ M.C.D.(36, 60) = 12 $$ Hai confermato il risultato anche con questo metodo!

A cosa serve conoscere il massimo comune divisore?

Il massimo comune divisore è una base fondamentale in molte aree della matematica e delle sue applicazioni.

Ad esempio, ti permette la riduzione delle frazioni.

Conoscere il M.C.D. permette di semplificare una frazione, riducendola ai minimi termini.

Esempio. Considera la frazione \(\frac{36}{60}\). Puoi semplificarla usando il massimo comune divisore. Come abbiamo calcolato in precedenza, il M.C.D. tra 36 e 60 è 12. Quindi, per ridurre la frazione, dividi sia il numeratore che il denominatore per il loro massimo comune divisore: $$ \frac{36 \div 12}{60 \div 12} = \frac{3}{5} $$ La frazione \(\frac{36}{60}\) ridotta ai minimi termini è \(\frac{3}{5}\). Lavorare con frazioni ridotte rende i calcoli più semplici e comprensibili.

Tuttavia, l'utilità del M.C.D. non si ferma qui.

Dietro a concetti apparentemente semplici, si celano anche strumenti matematici più complessi.

Ad esempio, il M.C.D. è utilizzato nello studio delle proprietà dei numeri interi, e gioca un ruolo importante in algoritmi di crittografia, dove è fondamentale trovare i numeri primi e loro relazioni.

Quindi, comprendere il M.C.D. è un primo passo per accedere a una matematica più avanzata.

Il legame tra il massimo comune divisore e il minimo comune multiplo

Il legame tra massimo comune divisore (M.C.D.) e minimo comune multiplo (m.c.m.) di due numeri \(a\) e \(b\) si esprime con la formula: $$ a \cdot b = M.C.D.(a, b) \cdot m.c.m.(a, b) $$

$$ Quindi, se conosci già il minimo comune multiplo di due numeri, puoi calcolare il massimo comune divisore anche in questo modo:

$$ M.C.D.(a, b)   = \frac{a \cdot b}{ m.c.m.(a, b) }  $$

Il M.C.D. è il prodotto dei fattori comuni con l’esponente più basso, mentre il m.c.m. è il prodotto di tutti i fattori (comuni e non), con l’esponente più alto.  Se \(a\) e \(b\) sono primi tra loro, il loro m.c.m. è semplicemente \(a \cdot b\). Questa relazione è valida per qualsiasi coppia di numeri interi e consente di calcolare uno dei due valori se si conosce il prodotto e l’altro valore.

Esempio

Prendiamo i numeri \(a = 12\) e \(b = 18\).

Fai la scomposizione in fattori primi dei due numeri

$$  a = 12 = 2^2 \cdot 3 $$

$$  b = 18 = 2 \cdot 3^2 $$

Calcola il M.C.D. prendendo i fattori comuni con l’esponente minore.

$$ M.C.D.(12, 18) = 2 \cdot 3 = 6 $$

Poi calcola il m.c.m. prendendo tutti i fattori con l’esponente più alto.

$$ m.c.m.(12, 18) = 2^2 \cdot 3^2 = 36 $$

Infine verifica la relazione tra il M.C.D. e il m.c.m.

$$ a \cdot b = M.C.D.(a, b) \cdot m.c.m.(a, b) $$

$$ 12 \cdot 18 = 6 \cdot 36 $$

Entrambi i membri sono uguali a 216, confermando che \( a \cdot b = M.C.D.(a, b) \cdot m.c.m.(a, b) \).

Pertanto, se conosci il minimo comune multiplo di due numeri $ m.c.m.(12, 18) = 36 $ di due numeri $ a $ e $ b $, puoi calcolare indirettamente anche il massimo comune divisore.

$$ M.C.D.(12, 18)   = \frac{12 \cdot 18}{ m.c.m.(12, 18) } = \frac{12 \cdot 18}{36} = \frac{18}{3} = 6  $$

E' un altro modo per calcolare il M.C.D.