I numeri irrazionali

Un numero irrazionale è un numero che non può essere espresso come rapporto tra due numeri interi.

La sua rappresentazione decimale è infinita e non periodica, ovvero le cifre dopo la virgola continuano all'infinito senza ripetersi in un pattern regolare.

Ciò significa che non esiste uno schema ripetuto di cifre. Questo lo rende "irraggiungibile" attraverso il semplice rapporto tra due interi, ed è proprio questa caratteristica che lo rende unico e un po' misterioso.

Ad esempio, la radice quadrata di 2 è un numero irrazionale

$$ \sqrt{2} = 1,414213562... $$

Per quanto tu possa impegnarti, non troverai mai due numeri interi \( a,b \in \mathbb{Z} \} in grado di ottenere la radice di 2.

$$ \sqrt{2} = 1,414213562... \ne \frac{a}{b}  \ \ \ a,b \ \in \ \mathbb{Z}  $$

Questo perché la parte decimale di un numero irrazionale è illimitata e non segue uno schema periodico.

In breve, i numeri irrazionali sfuggono alla rappresentazione come frazioni di numeri interi.

Perché sono detti irrazionali?

I numeri irrazionali prendono il loro nome dal fatto che non appartengono alla categoria dei numeri razionali, non perché siano "pazzi" o irregolari in senso caotico.

La parola "irrazionale" deriva dal latino irrationalis, che significa "non razionale" o "non esprimibile attraverso un rapporto".

Cos'è un numero razionale? Un numero razionale è un numero che può essere espresso come il rapporto tra due numeri interi, \( a/b \), con \( b \neq 0 \). La sua rappresentazione decimale può essere finita (come \( 0,5 \) per \( 1/2 \)) oppure infinita ma periodica, ossia con una sequenza di cifre che si ripete all'infinito (come \( 0,333... \) per \( 1/3 \)).

Esempi celebri di numeri irrazionali

Alcuni dei numeri irrazionali più noti sono:

• La radice quadrata di 2 (\( \sqrt{2} \)): Questo numero emerse per la prima volta nell'antica Grecia, quando i Pitagorici scoprirono che il rapporto tra la diagonale di un quadrato e il suo lato non poteva essere espresso come un numero razionale. La rappresentazione decimale di \( \sqrt{2} \) è \( 1,414213562...\), e le cifre continuano senza ripetersi.
• Pi greco (\( \pi \)): Questo numero rappresenta il rapporto tra la circonferenza di un cerchio e il suo diametro. È irrazionale (e trascendente, una categoria ancora più particolare) e il suo valore è circa \( 3,141592653...\), con cifre che sembrano casuali e non si ripetono.
• Il numero di Eulero (\( e \)): Fondamentale nel calcolo e nelle funzioni esponenziali, \( e \) è un altro numero irrazionale la cui rappresentazione decimale inizia con \( 2,718281828...\) e si estende infinitamente senza alcuna periodicità.

Sono solo alcuni esempi tra quelli più conosciuti e noti.

In realtà, i numeri irrazionali sono molti di più, sono infiniti.

Numeri irrazionali nella vita quotidiana. Potresti pensare che i numeri irrazionali siano relegati al mondo astratto della matematica, ma hanno applicazioni concrete in molte discipline. Ad esempio, in geometria, \( \pi \) è essenziale per calcolare aree e volumi di forme circolari. In fisica, \( e \) è fondamentale per descrivere fenomeni naturali come la crescita esponenziale e il decadimento radioattivo. In informatica, i numeri irrazionali possono apparire nei calcoli di precisione elevata.

L'insieme dei numeri irrazionali è infinito

I numeri irrazionali non sono rari o "eccezioni" nel mondo dei numeri reali.

Al contrario, sono onnipresenti: tra 0 e 1, ad esempio, esistono infiniti numeri irrazionali, e sono persino più "numerosi" dei numeri razionali, in un certo senso tecnico.

Questo concetto è legato alla teoria degli insiemi e alla cardinalità, dimostra che l'universo dei numeri irrazionali è straordinariamente ricco e vasto.

L'unione dell'insieme dei numeri irrazionali \( \mathbb{I} \) con quello dei numeri razionali \( \mathbb{Q} \) dà vita a un insieme ancora più grande, l'insieme dei numeri reali \( \mathbb{R} \).

$$ \mathbb{I} \cup \mathbb{Q} = \mathbb{R} $$

Come puoi vedere, l'unione di due o più insiemi infiniti genera un altro insieme infinito ma di "ordine superiore".

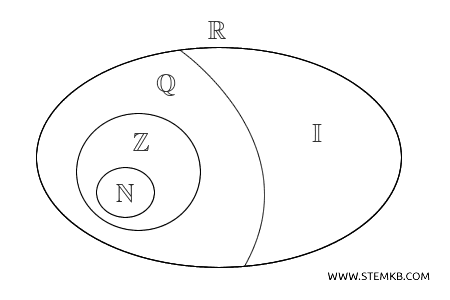
L'insieme dei numeri reali è l'insieme numerico che comprende tutti gli altri insiemi numerici: naturali \( \mathbb{N} \), interi \( \mathbb{Z} \), razionali \( \mathbb{Q} \) e irrazionali \( \mathbb{I} \).

Non pensare però che l'insieme dei numeri reali sia quello più grande... ce n'é un altro ancora più grande: l'insieme dei numeri complessi \( \mathbb{C} \). Ma di questo parleremo un'altra volta.

La scoperta dei numeri irrazionali

I primi ad accorgersi della scoperta dei numeri irrazionali furono i matematici e i filosofi della Scuola pitagorica,, fondata da Pitagora di Samo intorno al VI secolo a.C.

Si accorsero che la diagonale di un quadrato con lato unitario non può essere ottenuto come rapporto di due numeri.

Ad esempio, consideriamo un quadrato con lato unitario $ l = 1 $

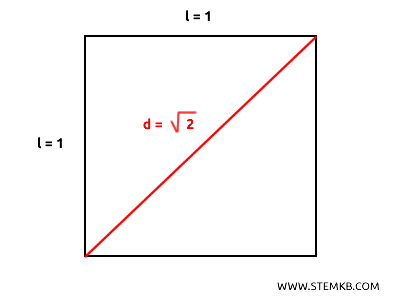
Per misurare la diagonale \( d \) possiamo usare il teorema di Pitagora.

$$ d^2 = 1^2 + 1^2 = 2 $$

Quindi, la diagonale del quadrato è la radice quadrata di due.

$$ d = \sqrt{2} $$

I pitagorici si accorsero che questo numero non poteva essere ottenuto tramite il rapporto di due numeri interi, quindi non era un numero razionale.

$$ \sqrt{2} = \frac{a}{b} $$

Dove il denominatore è diverso da uno \( b \ne 1 \) poiché \( \sqrt{2} \notin \mathbb{N} \) non è un un numero naturale.

Se per assurdo esistessero due numeri primi in grado di farlo, vorrebbe dire che il rapporto dei loro quadrati sarebbe uguale a 2.

$$ \frac{a^2}{b^2} = 2 $$

Questo però è impossibile perché vorrebbe dire che $ a $ è divisibile per $ b $, ma per l'ipotesi iniziale sono numeri primi.

Quindi, la radice quadrata di due non è un numero irrazionale ed è il primo numero irrazionale scoperto dall'uomo.

Ne seguirono molti altri $ \sqrt{3}, \sqrt{5}, \sqrt{7} $ e in generale ogni radice $ \sqrt{n} $ dove $ n $ non è un quadrato perfetto, il numero $ \pi $, ecc.

La scoperta dei numeri irrazionali fu un vero e proprio trauma per i Pitagorici, poiché credevano che tutto nell'universo fosse governato da proporzioni numeriche e che ogni cosa potesse essere rappresentata come il rapporto tra numeri interi. Quando uno dei membri della scuola, probabilmente Ippaso di Metaponto, dimostrò che la radice quadrata di 2 non poteva essere espressa come una frazione, fu un colpo devastante. Secondo alcune versioni, Ippaso fu persino punito, bandito o ucciso per aver rivelato il segreto dell'esistenza dei numeri irrazionali, poiché la scoperta fu considerata quasi eretica.

In conclusione, i numeri irrazionali, con le loro cifre infinite e non periodiche, aprono le porte a un mondo matematico che sfida la nostra intuizione e ci invita a esplorare oltre i limiti del razionale.

Come disse il matematico tedesco Leopold Kronecker: "I numeri naturali sono opera di Dio, tutto il resto è opera dell’uomo."

Ma i numeri irrazionali sembrano appartenere a una sfera ancora più alta, dove il caos e l'ordine si intrecciano in una danza infinita.