
I divisori di un numero
Immagina di avere due numeri, \( a \) e \( b \), con \( b \neq 0 \). Si dice che \( b \) è un divisore di \( a \) se, nel dividere \( a \) per \( b \), il resto della divisione è zero. In altre parole, \( b \) divide perfettamente \( a \) senza lasciare un resto. $$ a = q \cdot b $$ dove \( q \) è un numero naturale che rappresenta il quoziente della divisione di \( a \) per \( b \).
Quindi, se trovi un numero intero \( q \) tale che \( a = q \cdot b \), puoi dire che \( b \) è un divisore di \( a \).
È importante sottolineare che b deve essere diverso da zero \( b \neq 0 \).
La divisione per zero, infatti, non è definita: non possiamo dividere un numero per zero in matematica. Al contrario, qualsiasi numero \( n \) diverso da zero è divisore di zero, poiché \( 0 \div n \) dà quoziente e resto pari a zero.
Ad esempio \( 3 \) è un divisore di \( 12 \) perché \( 12 = 3 \cdot 4 \) e la divisione intera \( 12 \div 3 \) lascia come resto zero.
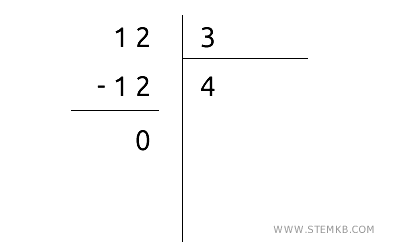
Per dire che \( b \) è un divisore di \( a \), esistono varie espressioni alternative:
- \( a \) è multiplo di \( b \)
- \( b \) divide \( a \)
- \( a \) è divisibile per \( b \)
Queste frasi sono intercambiabili e indicano tutte lo stesso rapporto divisorio tra \( a \) e \( b \).
Quindi, c'è una relazione molto stretta tra divisori e multipli: se \( b \) è un divisore di \( a \), allora \( a \) è un multiplo di \( b \) e viceversa.
A esempio, sapere che \( 12 \) è multiplo di \( 3 \) implica immediatamente che \( 3 \) è un divisore di \( 12 \), e viceversa.

Questa relazione è fondamentale in matematica perché collega in modo diretto la divisione alla moltiplicazione, e ci permette di capire meglio la struttura e le proprietà dei numeri.
Ricorda che a differenza dei multipli, i divisori di un numero sono finiti.
Per trovarli, devi considerare tutti i numeri che dividono perfettamente il numero in questione.
Ad esempio, i divisori di \( 12 \) sono:
$$ 1, \, 2, \, 3, \, 4, \, 6, \, 12 $$
Questi numeri dividono \( 12 \) senza lasciare resto e rappresentano tutti i possibili divisori di \( 12 \).
A cosa serve? Conoscere i divisori di un numero è essenziale per risolvere problemi aritmetici complessi e per affrontare concetti più avanzati, come la scomposizione in fattori primi o il calcolo del massimo comune divisore (MCD).
La rappresentazione dei divisori
Per rappresentare i divisori di un numero puoi usare il reticolo dei divisori.
Si tratta di una rappresentazione grafica utile per visualizzare i divisori di un numero e le loro relazioni gerarchiche.
In un reticolo dei divisori, i numeri più grandi sono collegati a quelli più piccoli in base alla divisibilità.
Ad esempio, nel reticolo dei divisori di \( 12 \), il numero \( 12 \) è collegato a tutti i suoi divisori (1, 2, 3, 4, 6) in base al fatto che ciascuno divide \( 12 \) perfettamente.
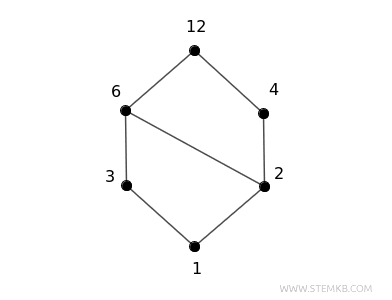
Spiegazione del reticolo. Al vertice del reticolo trovi il numero 12, che è il numero principale e viene diviso da tutti gli altri divisori. Al secondo livello ci sono 4 e 6 che sono divisori diretti di 12. Al terzo livello ci sono i numeri 2 e 3. Anche questi sono divisori di 12 ma sono anche divisori di 4 e 6. Per questa ragione sono a un livello inferiore. Infine, al livello più basso del reticolo c'è sempre il numero 1 che è il divisore di tutti i numeri.
Il reticolo dei divisori ti aiuta a visualizzare non solo i divisori di un numero, ma anche come questi si relazionano tra loro.

