
I numeri primi
I numeri primi sono i numeri naturali maggiori di 1 divisibili solo per 1 e per se stessi.
Ad esempio, 23 è un numero primo perché non ha altri divisori oltre a 1 e 23.
Un altro numero primo è il numero 7, perché è divisibile per 1 e per 7.
I numeri primi hanno da sempre affascinato matematici di ogni epoca.
La loro apparente semplicità nasconde infatti proprietà straordinarie, tanto che Euclide, già nel 300 a.C., dimostrò l’infinità dei numeri primi: per quanto si vada avanti a contare, ci sarà sempre un numero primo che ancora non è stato trovato. Più tardi, intorno al 200 a.C., il matematico greco Eratostene elaborò un metodo per individuare i numeri primi, noto come il crivello di Eratostene, un’idea tanto geniale quanto efficace, che viene utilizzata ancora oggi.
Viceversa, un numero composto è un numero che può essere scomposto in fattori primi, cioè è il prodotto di numeri primi.
Ad esempio, 18 è composto, perché può essere scritto come \( 2 \times 3 \times 3 \), dove sia 2 che 3 sono numeri primi.
Questa scomposizione, chiamata fattorizzazione, è un processo fondamentale per molti algoritmi di calcolo e per la crittografia.
L’infinità dei numeri primi
Il matematico greco Euclide dimostrò che i numeri primi sono infiniti con un ragionamento elegante.
Immagina di avere un elenco finito di numeri primi, per esempio 2, 3, 5, 7 fino a N.
Metti per ipotesi assurda che N sia il numero primo più alto.
Se li moltiplichi tutti insieme e aggiungi 1 al risultato, ottieni un nuovo numero che non può essere diviso da nessuno dei numeri della nostra lista perché il resto della divisione sarà sempre 1.
$$ P = ( 2 \times 3 \times 5 \times 7 \times ... \times N ) +1 $$
Questo numero P è sicuramente più grande di N.
$$ P > N $$
A questo punto ci sono due possibilità: il nuovo numero P è primo oppure è divisibile da altri numeri primi non inclusi nella lista iniziale.
- Se P è un numero primo allora N non è il numero primo più grande.
- Se P non è un numero primo, allora è divisibile per qualche altro numero primo diverso da 2, 3, 5, 7,..., N
In entrambi i casi, questo dimostra che il numero N non è il numero primo più grande di tutti.
Il risultato dimostra anche l'infinità dei numeri primi.
Il fascino dei numeri primi risiede proprio nel loro essere infiniti e imprevedibili, e proprio grazie a queste proprietà hanno un ruolo insostituibile nella matematica e nella tecnologia.
Il crivello di Eratostene
Per identificare i numeri primi fino a un certo limite, Eratostene ideò un metodo chiamato crivello di Eratostene.
Immagina di avere una lista di numeri da 2 fino a un certo numero \( n=50 \).
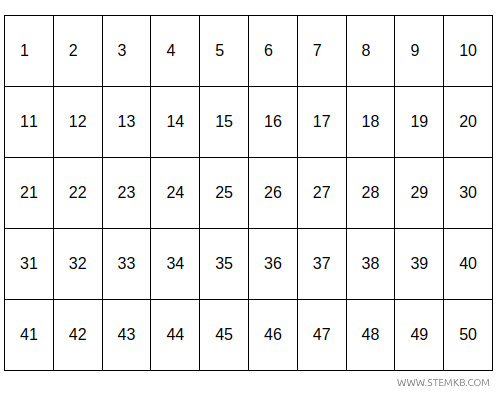
Si inizia escludendo il numero 1, poi si elimina ogni multiplo del numero 2 (ovvero tutti i numeri pari, eccetto 2 stesso).
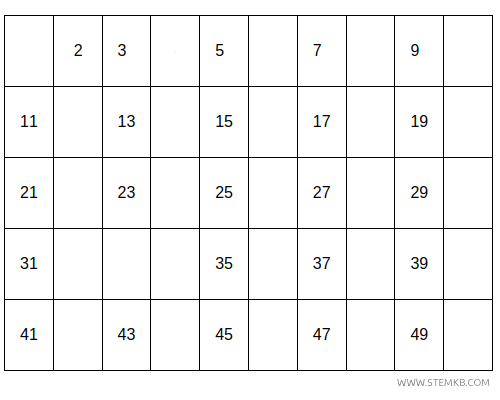
Poi ogni multiplo del numero 3.
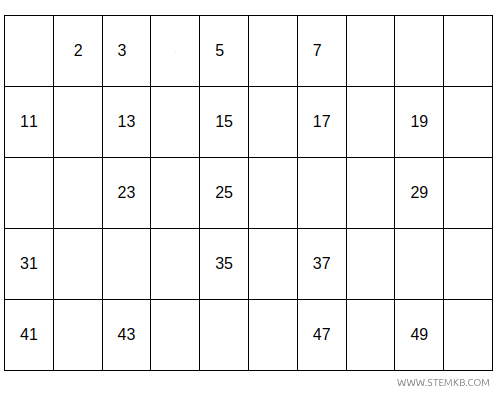
Poi ogni multiplo del numero 5.
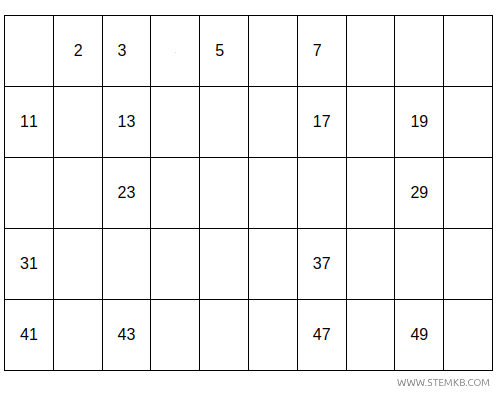
Poi ogni multiplo del numero 7.
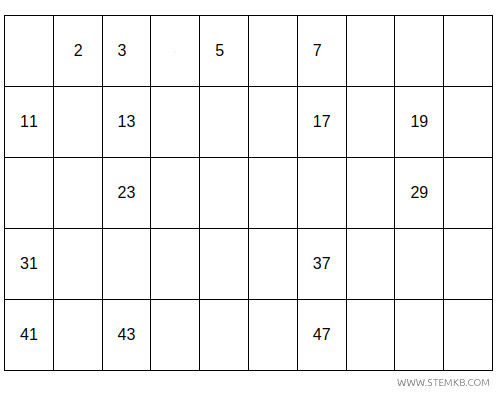
Poi ogni multiplo del numero 11.

Alla fine del processo, i numeri che rimangono sono primi.
Per esempio, con il crivello fino a 50, restano i numeri: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, e 47.
Le intuizioni di Euclide e Eratostene, che risalgono a millenni fa, continuano a guidarci nella scoperta di questi elementi fondamentali della nostra realtà numerica.
Il test di primalità
Per verificare se un numero è primo senza dividere per tutti i numeri minori, si usa un principio fondamentale: è sufficiente controllare i divisori fino alla radice quadrata del numero.
Dato un numero $ N $, se nessuno dei numeri primi fino alla radice quadrata $ \sqrt{N} $ divide esattamente $ N $, allora il numero $ N $ è primo.
Ad esempio, per verificare che 157 sia primo, basta controllare che non sia divisibile per i numeri primi minori o uguali a \(\sqrt{157} \approx 12.5\), ovvero 2, 3, 5, 7 e 11.
- \( 157: 2 = 78, \ \text{resto}=1 \)
- \( 157: 3 = 52, \ \text{resto}=1 \)
- \( 157: 5 = 31, \ \text{resto}=2 \)
- \( 157: 7 = 22, \ \text{resto}=3 \)
- \( 157: 11 = 14, \ \text{resto}=3 \)
Poiché nessuno di questi numeri primi divide 157, puoi dedurre che 157 è un numero primo.
In altre parole, non è necessario verificare che sia anche divisibile per gli altri numeri primi maggiori di 11.
Del resto considera il numero primo successivo a 11 che è 13. Se moltipli $ 13 \times 13 = 169 $ ottieni numero superiore a 157. Quindi 13 non può essere un divisore di 157. Lo stesso discorso vale per tutti gli altri numeri primi superiori alla radice quadrata di \(\sqrt{157} \approx 12.5\).
Importanza dei numeri primi nella matematica e nella crittografia
I numeri primi sono fondamentali nella matematica, in quanto costituiscono i mattoni dei numeri interi: ogni numero composto può essere scomposto in un prodotto unico di numeri primi.
Questa proprietà è alla base della crittografia moderna, in cui la sicurezza delle informazioni si basa sulla difficoltà di fattorizzare numeri molto grandi in fattori primi, un problema che richiede enormi risorse computazionali per essere risolto.
In conclusione, la semplicità dei numeri primi è solo apparente: questi numeri nascondono un mondo di misteri e applicazioni inimmaginabili, dai fondamenti dell’aritmetica fino alla sicurezza informatica.

