
Numeri interi
I numeri interi sono l'insieme dei numeri che comprendono tutti i numeri naturali (0, 1, 2, 3, ...) e i loro opposti negativi (-1, -2, -3, ...). L'insieme dei numeri interi si indica con il simbolo \(\mathbb{Z}\) e include tutti i numeri senza parte decimale o frazionaria. Questo insieme può essere scritto come: $$ \mathbb{Z} = \{ ..., -3, -2, -1, 0, 1, 2, 3, ... \} $$
I numeri interi rappresentano uno dei sistemi numerici fondamentali della matematica.
Formalmente, l’insieme dei numeri interi si indica con la lettera Z (dal termine tedesco Zahlen, che significa “numeri”), e si può esprimere così:
$$ Z = \{ \ldots, -3, -2, -1, 0, 1, 2, 3, \ldots \} $$
In questo insieme, lo zero funge da spartiacque: tutti i numeri alla sua destra (positivi) e quelli alla sua sinistra (negativi) sono numeri interi.
- Numeri positivi: Sono tutti i numeri interi maggiori di zero (1, 2, 3, …). Spesso, il segno “+” viene omesso nella scrittura dei numeri positivi, così che 3 e +3 rappresentano lo stesso valore.
- Numeri negativi: Rappresentano l’opposto dei numeri positivi e sono sempre minori di zero (-1, -2, -3, …). I numeri negativi vengono utilizzati in molti contesti pratici per indicare, ad esempio, temperature sotto lo zero o debiti finanziari.
- Zero: Lo zero è l’unico numero intero che non è né positivo né negativo. È l'elemento neutro dell'addizione, il che significa che aggiungendo zero a qualsiasi numero intero si ottiene lo stesso numero.
Questo dà origine a un sistema simmetrico in cui ogni numero positivo ha il suo opposto negativo.
Ad esempio, il numero opposto di 5 è -5 e viceversa. Il numero opposto di 6 e -6, ecc.
Esempio. Le temperature sotto lo zero vengono espresse con numeri interi negativi, mentre le temperature sopra lo zero sono positive. Ad esempio, -5 °C rappresenta una temperatura inferiore di cinque gradi rispetto al punto di congelamento dell’acqua. Un altro esempio di numeri interi sono i crediti e debiti sul conto corrente bancario di una persona. Un saldo di +50 euro indica un credito di 50 euro, mentre -50 euro indica un debito della stessa cifra.
Caratteristiche principali dei numeri interi
L'insieme dei numeri interi ha queste caratteristiche:
- Insieme infinito: L’insieme dei numeri interi non ha fine. Si estende all’infinito verso i numeri positivi e altrettanto verso i negativi, senza un limite massimo o minimo.
- Ordine: I numeri interi sono disposti in un ordine crescente e infinito sia in direzione positiva sia in direzione negativa, con lo zero al centro.
Immagina una linea dei numeri dove il punto zero è centrale, i numeri positivi sono disposti a destra e i negativi a sinistra. Questo aiuta a capire come gli interi rappresentano sia quantità positive che negative, come il saldo di un conto che può essere in attivo (positivo) o in debito (negativo).
In altre parole, dati due numeri interi a e b puoi sempre affermare che:
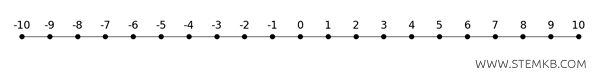
- a=b sono uguali se occupano lo stsso posto nella retta
- a<b se a è a sinistra di b sulla retta;
- a>b se a è a destra di b sulla retta.
- Discreto: L'insieme dei numeri interi è un insieme discreto perché, dati due numeri interi successivi, non si sono altri numeri interi tra di essi.
- Chiusura delle operazioni: L’insieme dei numeri interi è chiuso rispetto all’addizione, alla sottrazione e alla moltiplicazione. Questo significa che la somma, la differenza e il prodotto di due numeri interi sono sempre un numero intero. Ad esempio $$ 3 + 2 = 5 $$ $$ 3 -2 = 1 $$ $$ 3 \cdot 2 = 6 $$
L’insieme non è chiuso rispetto alla divisione. Per esempio, se dividi 3 per 2 non ottieni un numero intero, bensì un numero razionale (1,5). $$ 3 : 2 = 1,5 $$
- Numero opposto: Ogni numero intero ha un opposto (o inverso additivo) all'interno dell'insieme dei numeri interi. Ad esempio, l'opposto di 3 è -3. Quando sommi un numero con il suo opposto ottieni sempre zero. $$ 3+(-3)=0 $$
- Valore assoluto: Ogni numero intero ha un valore assoluto, che rappresenta la sua distanza dallo zero sulla retta numerica. Per esempio, il valore assoluto di -3 è 3, e quello di +3 è anch'esso 3. Il valore assoluto è sempre un numero positivo o zero. $$ | 3 | = |-3 | = 3 $$
Operazioni con i numeri interi
I numeri interi, pur sembrando semplici, richiedono attenzione nelle operazioni. Alcuni esempi delle regole più utili sono:
- Addizione e sottrazione: Quando sommi due numeri interi con lo stesso segno (numeri concordi), devi sommare i valori assoluti e mantenere lo stesso segno nel risultato. $$ 4 + 3 = +(|4|+|3|)=7 $$ $$ -4 + (-3) =-(|4|+|3|) = -7 $$ Quando, invece, stai sommando due numeri con segni opposti (numeri discordi), calcola la differenza tra i valori assoluti e mantieni il segno del numero con valore assoluto maggiore: $$ 5 + (-3) =+( |5|-|3|)= 2 $$ $$ -5 + 3 = -(|5|-|3|)= -2 $$
- Moltiplicazione e divisione: Il prodotto o il quoziente di due numeri interi si ottiene calcolando il prodotto o il quoziente dei loro valori assoluti, assegnando un segno positivo se i numeri sono concordi (stesso segno) e negativo se sono discordi (segno diverso). $$ 4 \cdot 3 = 12 $$ $$ -4 \cdot (-3) = 12 $$ $$ 4 \cdot (-3) = -12 $$
I numeri interi sono una parte essenziale della matematica e trovano applicazione in molte aree della vita quotidiana e della scienza.
Quindi, capire il loro comportamento e le regole per operare con i numeri interi ti permette di avere una base solida per affrontare anche concetti matematici molto più avanzati.

