Numeri razionali

Un numero razionale è un numero che può essere espresso come il rapporto di due numeri interi, $ \frac{a}{b} $, dove $ a $ e $ b $ sono interi e $ b \neq 0 $.

Il termine "razionale" deriva dal latino ratio, che significa "rapporto" o "ragione". Questo nome sottolinea la loro natura come rappresentazione di rapporti tra quantità.

Alcuni esempi di numeri razionali includono:

Interi come $ 5 $ che può essere scritto come $ \frac{5}{1} $
Frazioni come $ \frac{2}{3} $ o percentuali come $ \frac{75}{100} = 75\% $
Decimali finiti come $ 0,75 $ che è $ \frac{3}{4} $
Decimali periodici come $ 0,333... $ che corrisponde a $ \frac{1}{3} $ sia semplici che misti.

Da questo si capisce subito che gli interi ($ \mathbb{Z} $) sono un sottoinsieme dei razionali ($ \mathbb{Q} $), poiché ogni intero può essere scritto come una frazione con denominatore 1. Ad esempio, $ 5 = \frac{5}{1} $.

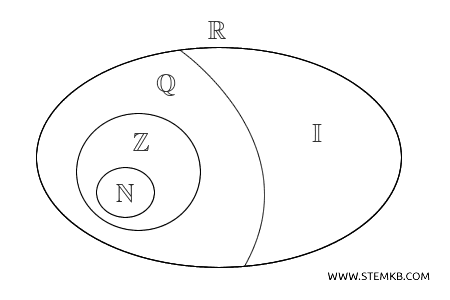
gli insiemi numerici

Tuttavia, i numeri razionali non bastano a descrivere tutti i numeri che possiamo immaginare perché, a loro volta, sono un sottoinsieme dei numeri reali ($ \mathbb{R} $).

Per esempio, non possono rappresentare la radice quadrata di 2, ossia $ \sqrt{2} $, quest'ultimo è un numero irrazionale (non razionale). Quindi, l'insieme dei numeri reali ($ \mathbb{R} $) possiamo vederlo come l'unione di due insiemi numerici distinti: l'insieme dei numeri razionali ($ \mathbb{Q} $) e l'insieme dei numeri irrazionali ($ \mathbb{I} $).

La proprietà dei numeri razionali

L'insieme dei numeri razionali $ \mathbb{Q} $ possiede molte proprietà interessanti e fondamentali nella teoria dei numeri e nell'algebra.

Insieme infinito
L'insieme dei numeri razionali è composto da infiniti numeri. Inoltre, è un insieme "infinitamente numerabile" perchè a ciascun numero razionale possiamo associare un numero naturale a ciascun numero razionale in modo da elencarli tutti.
Insieme ordinato
L'insieme dei numeri razionali è ordinato, il che significa che dati due numeri razionali $ q_1 $ e $ q_2 $, possiamo sempre stabilire una relazione di maggiore, minore o uguale. Questa caratteristica deriva dal fatto che è un insieme "numerabile".

Ad esempio, se prendiamo due numeri razionali $ \frac{1}{2} $ e $ \frac{3}{4} $, possiamo affermare che $ \frac{1}{2} < \frac{3}{4} $. Basta applicare il metodo del confronto incrociato delle proporzioni $ 1 \cdot 4 < 2 \cdot 3 $.
Densità
Tra due numeri razionali esiste sempre un altro numero razionale. Questo significa che la linea dei numeri razionali è "infinitamente densa". In altre parole, per ogni coppia di numeri razionali distinti tra loro $ q_1 < q_2 $, esiste sempre un numero razionale $ q_3 $ tale che $ q_1 < q_3 < q_2 $.
Ad esempio, tra $ \frac{1}{2} $ e $ \frac{3}{4} $, troviamo $ \frac{5}{8} $, $ \frac{9}{16} $, ecc. In altre parole, dati due numeri razionali distinti qualsiasi $ a $ e $ b $, la loro media $ c = \frac{a+b}{2} $ è ancora un numero razionale compreso tra $ a $ e $ b $.
Non completezza
Sebbene denso, l'insieme dei numeri razionali non è completo. Questo significa che esistono intervalli nei numeri razionali che non contengono tutti i numeri reali.
Un esempio classico è la radice quadrata di 2 ($ \sqrt{2} $), che non può essere rappresentata come frazione e quindi non appartiene a $ \mathbb{Q} $.
Addizione e moltiplicazione chiuse
L'insieme dei numeri razionali è chiuso rispetto ad alcune operazioni, il che significa che effettuando tali operazioni su due numeri razionali si ottiene sempre un altro numero razionale:
- Addizione: $ a/b + c/d = \frac{ad + bc}{bd} $ è ancora un numero razionale.
- Sottrazione: $ a/b - c/d = \frac{ad - bc}{bd} $ è un numero razionale.
- Moltiplicazione: $ a/b \cdot c/d = \frac{ac}{bd} $ è un numero razionale.
- Divisione: $ (a/b) \div (c/d) = \frac{ad}{bc} $, purché $ c \neq 0 $, è un numero razionale.
Ad esempio, la somma di $ \frac{1}{2} $ e $ \frac{3}{4} $ è ancora un numero razionale. $$ \frac{1}{2} + \frac{3}{4} = \frac{1 \cdot 2}{2 \cdot 2} + \frac{3}{4} = \frac{2}{4} + \frac{3}{4} = \frac{5}{4} $$
Periodicità decimale
I numeri razionali, se rappresentati come decimali, sono sempre finiti come $ 0,5 $ ($ \frac{1}{2} $) o $ 0,25 $ ($ \frac{1}{4} $) o periodici come $ 0,333... $ ($ \frac{1}{3} $) o $ 0,142857142857... $ ($ \frac{1}{7} $). Questo li distingue dai numeri irrazionali, come $ \pi $ o $ \sqrt{2} $, i cui decimali sono infiniti e non periodici. Sono essenziali per approssimare altri numeri.
Per esempio, possiamo avvicinarci arbitrariamente a un numero irrazionale come $ \pi $ usando numeri razionali, come $ \frac{22}{7} $ o $ \frac{355}{113} $.
Esistenza del reciproco
Per ogni numero razionale non nullo $ \frac{a}{b} \ne 0 $ esiste un numero razionale reciproco $ \frac{b}{a} $, tale che il loro prodotto è uguale a 1, l'elemento neutro della moltiplicazione. In altre parole $ \frac{a}{b} \cdot \frac{b}{a} = 1 $.
Ad esempio, se prendiamo il numero $ \frac{3}{2} $ anche il suo reciproco $ \frac{2}{3} $ è un numero razionale. $$ \frac{3}{2} \cdot \frac{2}{3} = 1 $$
Simmetrico rispetto allo zero
L'insieme dei numeri razionali include sia numeri positivi che negativi, oltre allo zero. Ciò significa che è simmetrico rispetto a zero. Se prendiamo un numero razionale $ q \in \mathbb{Q} $, allora anche il suo opposto $ -q \in \mathbb{Q} $ appartiene all'insieme dei numeri razionali.
Ad esempio, il numero $ \frac{1}{2} $ ha come opposto $ - \frac{1}{2} $ che è ancora un numero razionale. $$ \frac{1}{2} + (- \frac{1}{2} ) = 0 $$
L'insieme dei numeri razionali è un campo
L'insieme dei numeri razionali forma un campo, un'importante struttura algebrica. Ciò significa che $ \mathbb{Q} $ soddisfa le seguenti proprietà:
- Esistono elementi neutri per l'addizione (0) e la moltiplicazione (1)
- Ogni elemento ha un inverso additivo ($ -a/b $) e moltiplicativo ($ b/a $, purché $ a \neq 0 $)
- Le operazioni sono associative e commutative
- La moltiplicazione è distributiva rispetto all'addizione
Un campo è una struttura algebrica composta da un insieme di numeri (o altri oggetti) e alcune operazioni di base: sommare, sottrarre, moltiplicare e dividere (tranne per zero), e tutto funziona come ci aspettiamo, senza stranezze.

I numeri razionali sono la pietra angolare della matematica elementare, ma la loro importanza si estende ben oltre

La loro semplicità nasconde una ricchezza di applicazioni, che spazia dalla divisione di una torta alle teorie matematiche più complesse.