I numeri coprimi o relativamente primi

Quando si parla di numeri primi tra loro (o coprimi), ci si riferisce a due o più numeri naturali che non hanno alcun fattore divisore comune.

Questo significa che il massimo comune divisore (MCD) dei due numeri è uguale a 1.

In altre parole, non esiste nessun numero diverso da 1 che possa dividere entrambi i numeri esattamente.

Un esempio

Ad esempio, i numeri 12 e 13 sono primi tra loro, perché non condividono divisori comuni (a parte 1)

$$ MCD(12,13)=1 $$

Viceversa, i numeri 12 e 15 non sono primi tra loro, poiché condividono il divisore 3.

$$ MCD(12,15)=3 $$

Per determinare se due numeri sono coprimi, puoi utilizzare il metodo del massimo comune divisore (MCD) tramite l'algoritmo di Euclide

Come funziona l'algoritmo di Euclide

L'algoritmo di Euclide è uno dei metodi più efficienti per calcolare il MCD e si basa su una sequenza di divisioni successive, fino a ridurre uno dei numeri a zero.

Per calcolare l’MCD di due numeri \( a \) e \( b \) :

1. Dividi il numero maggiore per quello minore e calcola il resto.
2. Sostituire il numero maggiore con il numero minore e il numero minore con il resto appena calcolato.
3. Ripeti questo processo fino a ottenere un resto di zero.

Quando il resto è zero, il divisore utilizzato nell'ultimo passaggio è il MCD dei due numeri originali.

Se il MCD risulta uguale a 1, i numeri sono coprimi.

Esempio

Ad esempio, prendi in considerazione i numeri 12 e 13, e vedi se sono primi tra loro:

1. Dividi 13 per 12, ottieni un quoziente di 1 e un resto di 1.
2. Sostituisci 13 con 12 e 12 con 1.
3. Dividi 12 per 1, ottenendo un resto di 0.

Poiché hai ottenuto un resto di zero, l'ultimo divisore usato è 1 ed è il MCD.

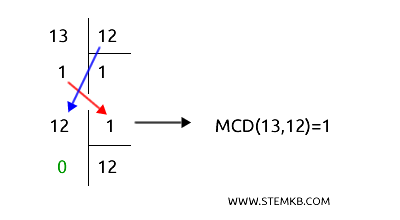
Questo conferma che 12 e 13 sono coprimi.

Esempio 2

Ripeti il procedimento con 12 e 15, invece:

1. Dividi 15 per 12, ottenendo un quoziente di 1 e un resto di 3.
2. Sostituisci 15 con 12 e 12 con 3.
3. Dividi 12 per 3, ottenendo un resto di 0.

In questo caso, l'ultimo divisore è 3, quindi il MCD di 12 e 15 è 3.

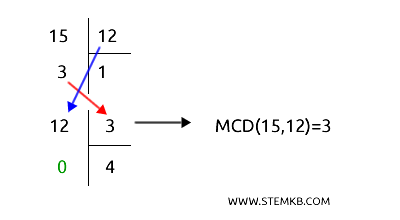
Dato che il MCD non è 1, questo significa che 12 e 15 non sono coprimi, perché hanno un divisore in comune.