L’insieme R dei numeri reali

Cosa sono i numeri reali?

Quando pensiamo ai numeri, immaginiamo una lunga sequenza di cifre che può continuare senza fine.

Tuttavia, c’è una differenza fondamentale tra i numeri che siamo abituati a maneggiare, come frazioni e interi, e quelli che appartengono a una realtà più vasta: i numeri reali, indicati con \( \mathbb{R} \).

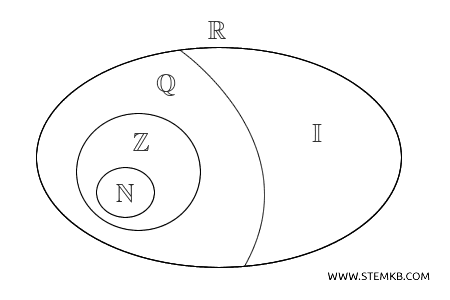
Questo insieme, che comprende sia i numeri razionali \( \mathbb{Q} \) che gli irrazionali \( \mathbb{I} \), costituisce un ponte tra il mondo discreto e l’infinito continuo.

Qual'è la differenza tra i numeri reali e i numeri razionali?

L’insieme dei numeri razionali, \( \mathbb{Q} \), è infinito e ordinato, ma non è completo.

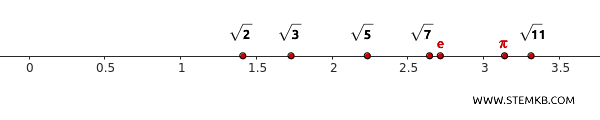
Ad esempio, esistono punti sulla retta come $ \sqrt{2} $, $ \sqrt{3}, o $ \pi $ che non corrispondono a nessun numero razionale.

In altre parole, se riportiamo i numeri razionali \( \mathbb{Q} \) sulla retta non copriamo tutti i punti, restano dei "buchi" non associati a nessun numero.

Un esempio celebre riguarda la diagonale di un quadrato di lato 1. Utilizzando il Teorema di Pitagora, scopriamo che la lunghezza della diagonale è \( \sqrt{2} \). Questo numero non può essere espresso come una frazione, poiché la sua rappresentazione decimale è infinita e non si ripete. Pertanto, \( \sqrt{2} \) è un numero reale irrazionale, che completa lo spazio lasciato “vuoto” dai numeri razionali.

L’insieme \( \mathbb{R} \) supera i limiti dei numeri razionali e colma questi "buchi" sulla retta.

Un punto chiave per comprendere la grandezza di \( \mathbb{R} \) è la sua proprietà di completezza: a ogni punto sulla retta corrisponde un numero reale, e a ogni numero reale corrisponde un punto sulla retta.

Questo rende \( \mathbb{R} \) un insieme che “riempie” completamente la linea continua.

In questo modo, l’insieme \( \mathbb{R} \) non è solo una collezione di numeri, ma una lente che ci permette di esplorare il mondo continuo sia nelle grandezze infinitamente grandi (più o meno infinito) che in quelle infinitamente piccole (infinitesimi).

Questo ci consente di analizzare fenomeni complessi e di avvicinarci a una comprensione più profonda della natura.

Le proprietà dell'insieme dei numeri reali

Vediamo nel dettaglio le principali proprietà dell'insieme dei numeri reali \( \mathbb{R} \).

• Illimitato
  L’insieme \( \mathbb{R} \) è un insieme infinito, ma di una grandezza superiore rispetto all’insieme dei numeri naturali \( \mathbb{N} \) o razionali \( \mathbb{Q} \) perché i numeri reali hanno una cardinalità non numerabile, che rappresenta un infinito “più grande” rispetto all’infinito numerabile dei numeri naturali. E' un insieme illimitato sia inferiormente ( \( - \infty \) ) che superiormente ( \( +\infty \) ).

  Ad esempio, immagina un numero reale qualsiasi $ n \in \mathbb{R} $. Potrai sempre trovare un altro numero reale $ M \in \mathbb{R} $ che è maggiore $ M > n $. Quindi, l'insieme dei numeri reali non ha un estremo superiore, ovvero è illimitato superiormente. Allo stesso modo, per ogni numero reale $ n $ puoi trovare anche un altro numero reale $ m \in \mathbb{R} $ che è minore di $ n $. Questo significa che l'insieme dei numeri reali non ha un estremo inferiore, ovvero è illimitato inferiormente.

• Ordinato
  L’insieme \( \mathbb{R} \) è un ordinato perché è possibile confrontare due numeri reali qualsiasi \( a \) e \( b \) e stabilire se \( a < b \), \( a = b \), o \( a > b \). Questo ordinamento consente di rappresentare i numeri reali su una retta numerica, dove ogni numero ha una posizione ben definita.
• Denso
  L’insieme dei numeri reali è denso perché tra due numeri reali \( a \) e \( b \) (con \( a < b \)) esiste sempre un altro numero reale \( c \) tale che \( a < c < b \).  Questa proprietà si applica anche ai numeri razionali, ma nel caso di \( \mathbb{R} \), include sia numeri razionali che irrazionali.
• Completo
  L'insieme dei numeri reali \( \mathbb{R} \) è completo perché ogni punto sulla retta numerica corrisponde a un numero reale, e viceversa. La proprietà di completezza distingue \( \mathbb{R} \) dall’insieme dei numeri razionali \( \mathbb{Q} \). 
• Continuo
  Dal punto di vista topologico, l'insieme dei numeri reali \( \mathbb{R} \) soddisfa anche la proprietà della continuità. perché non ci sono “buchi” nella retta reale. In altre parole, \( \mathbb{R} \) forma un continuum.

Ora vediamo nel dettaglio quali sono le proprietà algebriche dei numeri reali.

L’insieme \( \mathbb{R} \) è dotato di operazioni algebriche come somma e prodotto, e soddisfa le seguenti proprietà:

• Chiusura
  La somma e il prodotto di due numeri reali sono sempre numeri reali. Questo garantisce che l’insieme \( \mathbb{R} \) rimanga autosufficiente e coerente sotto queste operazioni.
• Associatività
  E' una proprietà che assicura che il risultato delle operazioni non dipenda dall’ordine in cui vengono eseguite. $$ (a + b) + c = a + (b + c) $$ $$ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$
• Commutatività
  E' un principio che sottolinea la simmetria delle operazioni di somma e prodotto nei numeri reali. $$ a + b = b + a $$ $$ a \cdot b = b \cdot a $$
• Elemento neutro
  Esistono due numeri speciali \( 0 \) e \( 1 \) detti "neutri" rispettivamente nei confronti dell'addizione e della moltiplicazione, che non alterano il risultato delle operazioni. $$ a + 0 = a $$ $$ a \cdot 1 = a $$
• Elemento inverso
  Per ogni \( a \neq 0 \), esiste un numero reale \( \frac{1}{a} \) tale che \( a \cdot \frac{1}{a} = 1 \), un meccanismo che consente di annullare effetti moltiplicativi.
• Distributività
  E' una proprietà che collega moltiplicazione e somma, permettendo di semplificare espressioni algebriche e gestire calcoli distribuiti. $$ a \cdot (b + c) = a \cdot b + a \cdot c $$

In conclusione, l'insieme dei numeri reali è un sistema numerico che va oltre i numeri razionali e consente di modellare fenomeni continui con maggiore precisione.

L'insieme dei numeri reali, per quanto vasto e completo, non rappresenta il limite massimo tra i sistemi numerici. Esiste infatti un'estensione ancora più ampia e potente: l'insieme dei numeri complessi \( \mathbb{C} \), che arricchisce il nostro universo matematico con nuove dimensioni di calcolo e rappresentazione.