La proprietà distributiva della moltiplicazione rispetto all'addizione

La proprietà distributiva della moltiplicazione rispetto all'addizione afferma che, dati tre numeri \( a \), \( b \) e \( c \): $$ a \times (b + c) = (a \times b) + (a \times c) $$

In altre parole, moltiplicare un numero per la somma di due altri numeri è lo stesso che moltiplicare quel numero per ciascuno dei due e poi sommare i risultati.

Pensala come un "trucco" per semplificare calcoli  e per risolvere espressioni algebriche che sembrano più difficili di quanto siano in realtà, distribuendo la moltiplicazione su ciascun termine dell'addizione.

Ricorda che la proprietà distributiva della moltiplicazione si applica anche nel caso della sottrazione. $$ a \times (b - c) = (a \times b) - (a \times c) $$

Esempio

Immagina di essere al mercato, e hai bisogno di comprare delle mele e delle pere.

Supponiamo che le mele costino 2 euro l'una e le pere costino 3 euro l'una.

Vuoi comprare 4 mele e 4 pere. Per sapere il costo moltiplichi il costo delle 4 mele (2 euro per 4) e poi quello delle 4 pere (3 euro per 4) e sommi i due risultati.

$$ 2 \times 4 + 3 \times 4 $$

Ma c’è un altro modo di pensare a questo problema: puoi fare due calcoli separati.

Cioè, sommi prima il costo di una mela (2 euro) e di una pera (3 euro) e poi moltiplichi il totale per le 4 unità che vuoi comprare.

$$ (2 + 3) \times 4 $$

Ora, perché queste due operazioni sono equivalenti? Perché la proprietà distributiva dice che:

$$ a \times (b + c) = a \times b + a \times c $$

In questo caso, "a" è il numero 4, mentre "b" e "c" sono i prezzi delle mele e delle pere.

La proprietà distributiva ti dice che puoi distribuire la moltiplicazione su ciascun termine dell’addizione e poi sommare.

Se non sei ancora convinto, prova a eseguire i calcoli passo dopo passo. Se calcoli \((2 + 3) \times 4\), ottieni 20. $$ 5 \times 4 = 20 $$Ora, calcola invece i due termini separatamente, ossia \((2 \times 4) + (3 \times 4)\): $$ 8 + 12 = 20 $$ Come puoi vedere, il risultato è identico: 20 in entrambi i casi! Questo dimostra come la proprietà distributiva funzioni, indipendentemente dal modo in cui si eseguono i calcoli.

Esempio 2

Facciamo un altro esempio con la sottrazione. Considera \( a = 3 \), \( b = 8 \) e \( c = 5 \).

$$ 3 \times (8 - 5) = 3 \times 3 = 9 $$

Ora applichiamo la proprietà distributiva:

$$ 3 \times (8 - 5) = (3 \times 8) - (3 \times 5) = 24 - 15 = 9 $$

Entrambi i risultati sono uguali, perché la proprietà distributiva funziona anche con la sottrazione.

La spiegazione geometrica

La proprietà distributiva della moltiplicazione rispetto all'addizione si può spiegare anche in termini geometrici utilizzando l'area di un rettangolo,.

Immagina un rettangolo con un'area totale pari a \( a \cdot (b + c) \).

Questo significa che la base del rettangolo è \( a \) e l'altezza è \( b + c \), quindi l'area totale è calcolata come \( a \cdot (b + c) \).

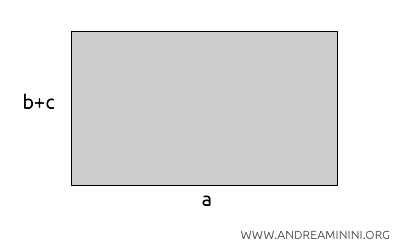
Lo stesso rettangolo puoi scomporlo in due rettangoli più piccoli.

Uno ha altezza \( b \) e area \( a \cdot b \), mentre l'altro ha altezza \( c \) e area \( a \cdot c \).

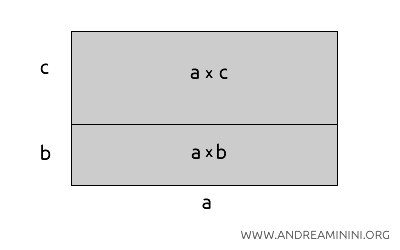
La somma delle aree dei due rettangoli è quindi \( a \cdot b + a \cdot c \).

Poiché la superficie del rettangolo è sempre la stessa, è evidente che le due espressioni sono equivalenti.

$$ a \cdot (b + c) = a \cdot b + a \cdot c $$

Questa scomposizione mostra visivamente come la moltiplicazione distributiva funzioni: l'area totale del rettangolo iniziale \( a \cdot (b + c) \) è la stessa somma delle aree dei due rettangoli più piccoli, confermando che \( a \cdot (b + c) = a \cdot b + a \cdot c \).

Ma perché tutto questo dovrebbe importarci?

Perché usare la proprietà distributiva può semplificare i calcoli, soprattutto quando i numeri diventano grandi. È come avere una scorciatoia per evitare di fare passaggi complessi e risolvere i problemi in modo più rapido.

Puoi usarla in un verso oppure nell'altro a seconda di come ti fa comodo.

Ti faccio un esempio concreto.

Immagina di dover calcolare questa espressione matematica.

$$ 17 \times 3 + 23 \times 3 $$

Puoi calcolare il costo totale facendo due calcoli separati: $ 17 \times 3 = 51 \quad \text{e} \quad 23 \times 3 = 69 $. Poi sommare i risultati:

$$ 51 + 69 = 120 $$

Ma puoi rendere tutto più semplice usando la proprietà distributiva.

Poiché entrambe le quantità (17 e 23) sono moltiplicate per lo stesso numero (3), puoi sommare prima i due valori e poi moltiplicare:

$$ (17 + 23) \times 3 $$

$$ 40 \times 3 = 120 $$

In questo modo, anziché fare due moltiplicazioni e poi una somma, fai una somma e una sola moltiplicazione.

La somma ti restituisce un numero con lo zero finale (40) e la moltiplicazione per 3 diventa molto più semplice.

In pratica, spesso la proprietà distributiva ti aiuta a svolgere i calcoli più rapidamente e ti aiuta a evitare errori, soprattutto quando i numeri diventano più grandi.