L'addizione

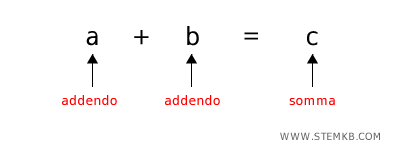
L'addizione è l'operazione aritmetica che consiste nel combinare due o più quantità per ottenere un'unica quantità, chiamata somma. Se hai due numeri, \( a \) e \( b \), l'addizione si scrive come \( a + b \), e il risultato è la somma di \( a \) e \( b \).

In parole povere, l'addizione è l'operazione matematica che consiste nel mettere insieme due o più numeri per ottenere un risultato. Sembra facile, vero? E lo è.

Ma ovviamente ci sono termini specifici che dobbiamo usare.

• Addendi: Sono i numeri che sommi. Se stai facendo 2 + 3, sia 2 che 3 sono gli addendi.
• Somma: Questo è il risultato dell'addizione. Se sommi 2 e 3, ottieni 5. Quel 5 è la somma.

Facciamo un esempio giusto per essere sicuri che sia tutto chiaro.

$$  2 + 3 = 5 $$

In questo esempio, i numeri 2 e 3 sono gli addendi e il 5 è la somma.

Ora, se ti chiedi “tutto qui?”. No, ovviamente no. Vediamo cosa succede quando le cose si complicano un pochino di più.

Addizione con più addendi

A volte devi mettere insieme più addendi. Ma tranquillo, il principio è lo stesso. Basta che continui ad aggiungere, uno alla volta.

Ad esempio, prova a sommare quattro numeri.

$$  1 + 2 + 3 + 4 = 10 $$

In questo caso, hai quattro addendi (1, 2, 3 e 4), e il risultato finale, 10, è la somma. Vedi? Niente di troppo complicato.

Proprietà dell'addizione

L'addizione ha delle proprietà che devi assolutamente conoscere.

• Proprietà commutativa: In soldoni, non importa l'ordine in cui sommi i numeri, il risultato sarà sempre lo stesso.

  Ad esempio $$ 2 + 3 = 3 + 2 $$ In entrambi i casi, la somma è 5.

• Proprietà associativa: Quando sommi più di due numeri, puoi raggrupparli come preferisci, e la somma non cambierà.

  Ad esempio $$ (1 + 2) + 3 = 1 + (2 + 3) $$ In entrambi i casi, la somma è 6.

• Elemento neutro (o Identità additiva): Se aggiungi zero a un numero, il numero non cambia. Zero è l'elemento neutro dell'addizione.

  Ad esempio $$ 5 + 0 = 0+5 = 5 $$

• Elemento opposto: Nell'insieme dei numeri interi $ \mathbb{Z} $, ogni numero intero $ a $ ha un numero opposto $ -a $. La somma di due numeri opposti è sempre uguale a zero $ a + (-a) =0 $ ossia all'elemento neutro dell'addizione.

  Ad esempio $$ 5 + (-5) = 5-5 = 0 $$

L'addizione tra numeri relativi

Quando sommi dei numeri relativi (numeri con segno più o meno), devi seguire queste regole:

• Somma di due numeri con lo stesso segno (numeri concordi)
  Il risultato è un numero con lo stesso segno degli addendi.  Il valore assoluto del risultato è la somma dei valori assoluti degli addendi.

  Ad esempio, la somma tra \( +2 \) e \( +3 \) è: $$ 2 + 3 = +(|2| + |3|) = +5 $$ La somma tra \( -2 \) e \( -3 \) è:
  $$ (-2) + (-3) = -(|-2| + |-3|) = -(2 + 3) = -5 $$

• Somma di due numeri con segno diverso (numeri discordi)
  Il risultato ha il segno del numero con valore assoluto maggiore. Il valore assoluto del risultato è la differenza tra il valore assoluto maggiore e quello minore.

  Ad esempio, la somma tra \( -2 \) e \( +3 \) è: $$ -2 + 3 = +(|3| - |2|) = +(3 - 2) = +1 $$ La somma tra \( +2 \) e \( -3 \) è: $$ 2 + (-3) = -(|3| - |2|) = -(3 - 2) = -1 $$

• Somma di due numeri opposti
  La somma di due numeri opposti è sempre zero.

  Ad esempio, la somma tra \( -2 \) e \( +2 \) è zero: $$ -2 + 2 = 0 $$ La somma tra \( +2 \) e \( -3 \) è: $$ 2 + (-3) = -(|3| - |2|) = -(3 - 2) = -1 $$

Addizione con numeri negativi

Ora, questa parte può fare confusione. Se aggiungi numeri negativi, è come sottrarre.

Ad esempio, se sommi 5 e -3 il risultato è la differenza.

$$ 5 + (-3) = 2 $$

Perché questo accade? In questi casi è come se ci fosse un "1" nascosto dopo il segno + che moltiplica il numero negativo (-3)

$$ 5 + 1 \cdot (-3)  $$

La moltiplicazione tra un numero positivo e uno negativo è sempre un numero negativo.

$$ 5 -3 = 2 $$

Semplice, no? È solo una sottrazione travestita da addizione. Quindi, non lasciarti ingannare dai segni meno.

Addizione con decimali e frazioni

Ah, vuoi fare il brillante e sommare i decimali o le frazioni? Certo, nessun problema. Solo un po’ di attenzione in più:

Ad esempio, puoi sommare due numeri con i decimali mettendo i numeri in colonna.

$$ 2,5 + 1,75 = 4,25 $$

Somma i numeri in colonna partendo dalla cifra più a destra. Se la somma di una colonna supera 9, riporta la cifra delle decine alla colonna immediatamente successiva a sinistra.

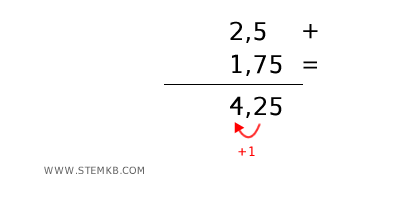
Per sommare le frazioni, invece, basta trovare un denominatore comune e il gioco è fatto.

$$ \frac{1}{2} + \frac{1}{4} =      \frac{2+1}{4}  =  \frac{3}{4}  $$

L'addizione è un'operazione chiusa nei numeri naturali

Questo vuole dire che se sommi due numeri naturali, il risultato sarà ancora un numero naturale.

Ad esempio, se sommi 3 e 5 il risultato è 8 che è un altro numero naturale.

$$ 3 +  5 = 8 $$

Non importa quali numeri naturali scegli, la loro somma sarà sempre un altro numero naturale.

Questa proprietà è anche detta "chiusura dell'insieme dei numeri naturali rispetto all'addizione".

Ricorda che i numeri naturali sono quei numeri che usi abitualmente per contare. Ad esempio, 0, 1, 2, 3, 4, 5, ecc. $$ \mathbb{N} = \{ 0, 1, 2, 3, 4, 5, 6, ... \}  $$

In conclusione, l'addizione è la più semplice delle operazioni, ma anche la base per costruire tutto il resto. Se capisci bene questa, sei già a metà dell'opera.