Sottrazione

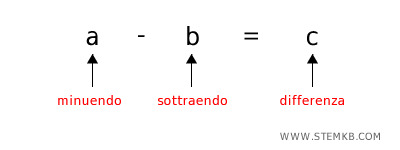
La sottrazione è l'operazione matematica che consiste nel togliere una quantità da un'altra per determinare la differenza tra due numeri. Si esprime come $$ a - b = c $$ Dove "a" è il numero da cui sottrai (minuendo), "b" è quanto togli (sottraendo), e "c" è il risultato (differenza).

Quindi, la differenza (c) tra due numeri è un numero naturale che addizionato al sottraendo (b) dà come risultato il minuendo (a). $$ a+c=b $$

La sottrazione è ovunque: quando controlli il saldo del conto corrente dopo aver fatto degli acquisti, quando togli dei libri da uno scaffale, o anche quando sottrai il tempo che manca per finire un lavoro.

Ti faccio un esempio.

Immagina di avere 10 biscotti. Bene, ecco che arriva il momento della sottrazione: decidi di mangiarne 3.

La domanda è: quanti te ne restano? Beh, facile: 10 meno 3 fa 7. Voilà, hai appena fatto una sottrazione!

$$ 10 - 3 = 7 $$

In questo esempio 10 è il minuendo, 3 è il sottraendo e 7 è la differenza.

Vuoi vedere un altro esempio?

Diciamo che tu abbia 20 euro e spendi 6 euro per un libro e altri 8 euro per una pizza. Quanti soldi ti restano? Beh, prima togli il costo del libro:

$$ 20 - 6 = 14 $$

Poi togli il costo della pizza:

$$ 14 - 8 = 6 $$

Alla fine, ti restano 6 euro. Vedi come ogni sottrazione riduce un po’ alla volta ciò che avevi all’inizio?

Ora, ci sono alcune cose interessanti da notare.

Cosa succede se provi a sottrarre un numero più grande da uno più piccolo?

Ecco che entriamo nel regno dei numeri negativi!

Supponiamo di avere 5 biscotti, ma per qualche motivo tu abbia promesso 8 biscotti a un amico. Ora hai un problema:

$$ 5 - 8 = -3 $$

Cosa significa questo meno 3? In pratica, significa che sei in debito di 3 biscotti con il tuo amico.

È un concetto che si estende anche a cose come i conti bancari: se hai speso più soldi di quanti ne avevi, finisci in rosso, cioè in debito.

La sottrazione come operazione inversa dell'addizione

Un altro modo divertente per pensare alla sottrazione è come l'operazione inversa dell'addizione.

Ad esempio, se 7 meno 3 dà 4

$$ 7 - 3 = 4 $$

Puoi pensarla al contrario: se prendi quel 4 e ci aggiungi 3, ottieni di nuovo 7.

$$ 4 + 3 = 7 $$

Quindi una volta che capisci che puoi "invertirla" con l'addizione, diventa davvero un gioco molto utile! 

La sottrazione dei numeri relativi

La differenza tra due numeri interi relativi è la somma del primo numero (minuendo) per l'opposto del secondo numero (sottraendo)

$$ a-b=a+(-b) $$

In questo modo, la sottrazione dei numeri relativi viene ricondotta all'addizione senza aggiungere altre regole.

A differenza dei numeri naturali, la sottrazione è un'operazione interna ai numeri interi e, in generale, ai numeri reali.

Questo vuol dire che la differenza tra due numeri interi è ancora un numero intero.

$$ 3 - 5 = 3 + (-5) = -2 $$

In generale, la sottrazione è chiusa anche nell'insieme dei numeri reali.

Le proprietà della sottrazione

Qui le cose si fanno interessanti, perché, a differenza dell'addizione, la sottrazione è un po’ più esigente. Non si comporta sempre come ti aspetteresti.

Ma non preoccuparti, ci sono solo alcuni punti chiave da tenere a mente:

• Proprietà invariantiva della sottrazione
  La differenza di due numeri $ a - b $ non cambia se si sottrae o si aggiunge a entrambi uno stesso numero $ c $. $$ a-b = (a-c)-(b-c) $$ $$ a+b = (a+c)-(b+c) $$

  Esempio. La differenza tra 10-6 è 4. Se sommi 3 sia al minuendo che al sottraendo la differenza non cambia. $$ (10+3)-(6+3)=13-9= 4 $$ Allo stesso modo, se sottrai 3 sia al minuendo che al sottraendo la differenza è sempre la stessa. $$ (10-3)-(6-3)=7-3= 4 $$

• Non è commutativa
  La commutatività è una proprietà che funziona a meraviglia con l'addizione: se dici che \(5 + 3 = 8\), allora anche \(3 + 5 = 8\). L'ordine non cambia il risultato. È come se i numeri dicessero: "Ok, tu vai prima e io dopo, oppure io vado prima e tu dopo, tanto arriviamo sempre allo stesso posto". Ma con la sottrazione, niente di tutto questo! Prova a sottrarre 5 da 3:  $$ 3 - 5 = -2 $$ E ora prova a invertire l'ordine, sottraendo 3 da 5:  $$ 5 - 3 = 2 $$ Oh oh! Vedi cosa succede? I risultati sono diversi! Questo significa che la sottrazione non è commutativa. Non puoi scambiare l'ordine dei numeri come ti pare, perché cambia tutto.
• Non è associativa
  L'addizione ti permette anche di raggruppare i numeri come vuoi, grazie alla sua bella proprietà associativa: $$ (2 + 3) + 4 = 2 + (3 + 4) $$ $$ 5+4 = 2+7 $$ $$ 9 = 9 $$ Nella sottrazione, però, le cose vanno diversamente. Guarda qui:  $$ (10 - 5) - 2 $$ $$ 5 - 2 = 3 $$ Ma se provi a raggruppare diversamente ottieni un altro risultato:  $$ 10 - (5 - 2) $$ $$ 10 - 3 = 7 $$ Quindi, la sottrazione non è associativa. Non puoi semplicemente spostare le parentesi come fai con l'addizione, perché cambia tutto.
• L'elemento neutro
  Ogni operazione ha il suo "elemento neutro", che è quel numero che non cambia nulla. Nell'addizione è lo zero, e anche nella sottrazione, guarda caso, lo zero ha il suo ruolo. Se sottrai zero da un numero, non cambia nulla. $$ a - 0 = a $$ Se hai 10 mele e nessuno te ne toglie, restano sempre 10 mele. Facile, no?

  Ma attenzione! Se fai l'operazione inversa, cioè se togli il numero da se stesso, ottieni zero:  \(a - a = 0\) Questo è come dire: "Ho 5 mele e mi prendo tutte e 5 le mele". E cosa rimane? Nulla, zero! Del resto, la sottrazione non è un'operazione commutativa. Ne abbiamo parlato poco fa.

• La sottrazione di numeri negativi
  Ecco dove la sottrazione comincia a giocare scherzi interessanti. Che succede se sottrai un numero negativo? Ti viene in mente quella famosa battuta: "Due negazioni fanno un’affermazione"? Beh, in matematica è vero! Se hai $$ 5 - (-3) $$ Questo è come dire: “Sto togliendo un debito”. E cosa succede quando togli un debito? Ti ritrovi con più soldi! Quindi $$ 5 - (-3) = 5 + 3 = 8 $$ In pratica, sottrarre un numero negativo è come aggiungerlo.

  Un consiglio. Quando ti trovi davanti a una sottrazione con un numero negativo al sottraendo $$ 5 - (-3) $$ immagina che tra il segno meno e la parentesi aperti sia sottinteso un $ 1 \times $ $$ 5 - 1 \times (-3) $$ In algebra il prodotto tra due numeri negativi è un numero positivo. Quindi, la moltiplicazione tra -1 e -3 dà come risultato 3. $$ 5 + 3 $$ In questo modo hai ricondotto tutto a una somma e il risultato è più chiaro $$ 5+3 = 8 $$

• Non è un'operazione chiusa con i numeri naturali
  Ora, parliamo di un’altra questione interessante. Se fai una sottrazione tra due numeri naturali (tipo 5 - 3=2), ti trovi ancora nel mondo dei numeri naturali, quei numeri che usiamo per contare (0,1,2,3,...). Ma se provi a sottrarre un numero più grande da uno più piccolo (come 3 - 5 = -2), ecco che entri nel mondo dei numeri negativi che non sono "naturali".

  La sottrazione, quindi, può portarti fuori dall'insieme dei numeri naturali e spingerti nei territori dei numeri negativi. Non è sempre garantito che rimani nello stesso "insieme" di numeri, e questo dipende proprio dai valori che scegli. Per questa ragione si dice che la sottrazione "non è un'operazione chiusa" con i numeri naturali.

Riassumendo, la sottrazione è una specie di "ribelle" in matematica. Non segue sempre le stesse regole dell'addizione, è un po’ più complicata e ti obbliga a fare attenzione a dove metti i numeri e in che ordine li lavori.

Però, una volta capite le sue "esigenze", diventa uno strumento fondamentale e ti apre le porte a concetti più avanzati, come i numeri negativi, che sono incredibilmente utili per spiegare tantissimi fenomeni nel mondo reale.