
La moltiplicazione
La moltiplicazione è una delle quattro operazioni aritmetiche fondamentali, insieme all'addizione, alla sottrazione e alla divisione. Rappresenta l'addizione ripetuta di uno stesso numero e ha applicazioni innumerevoli nella vita quotidiana e in vari campi della scienza.
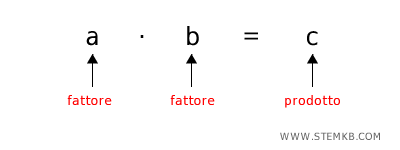
Il simbolo della moltiplicazione è il "×" (per) nei testi più semplici o il punto centrato "·" contesti più formali e avanzati.
In termini semplici, la moltiplicazione è un modo rapido per aggiungere lo stesso numero a sé stesso un certo numero di volte.
Quando moltiplichi, i numeri coinvolti si chiamano fattori. E il risultato? Si chiama prodotto.
Ad esempio, 4 × 3 equivale a sommare il numero 4 per 3 volte:
$$ 4 × 3 = 4 + 4 + 4 = 12 $$
In questo caso 4 e 3 sono i fattori mentre 12 è il prodotto, il frutto di tanto inutile sforzo mentale.
Ammettiamolo, imparare a moltiplicare non è solo una tortura scolastica, serve anche nella vita reale. La comprensione della moltiplicazione è fondamentale nella vita quotidiana. Dalle semplici spese al supermercato ai complessi calcoli scientifici, la moltiplicazione è uno strumento indispensabile. Quindi, puoi fare a meno di molte cose nella vita, ma non della moltiplicazione.
Proprietà della moltiplicazione
La moltiplicazione soddisfa diverse proprietà della matematica:
- Proprietà commutativa
L'ordine dei fattori non cambia il prodotto. Ovvero, puoi girare i numeri come ti pare, il risultato è lo stesso. $$ 4 \times 3 = 3 \times 4 = 12 $$ Tipo quando cambi posto ai mobili ma il tuo salotto è ancora terribile. - Proprietà associativa
Il modo in cui i fattori sono raggruppati non cambia il prodotto. $$ (2 \times 3) \times 4 = 2 \times (3 \times 4) $$ $$ 6 \times 4 = 2 \times 12 $$ $$ 24 = 24 $$ Quindi, se vuoi complicarti la vita con le parentesi, fai pure. Ma sappi che non cambia niente. - Proprietà distributiva
La moltiplicazione si distribuisce sull'addizione. In altre parole, se moltiplichi ogni addendo e poi sommi i prodotti, il risultato è sempre lo stesso. $$ 2 \times (3+4) = (2 \times 4) + (2 \times 4) $$ $$ 2 \times 7 = 6 + 8 $$ $$ 14=14 $$La proprietà distributiva della moltiplicazione si applica anche alla sottrazione. $$ 2 \times (5 - 3) = (2 \times 5) - (3 \times 2) $$ $$ 2 \times 2 = 10 - 6 $$ $$ 4 = 4 $$
Poi devi considerare che la moltiplicazione ha un elemento neutro ed è il numero 1, perché moltiplicare un numero per 1 non cambia il suo valore.
$$ 5 \times 1 = 5 $$
Inoltre, ha anche un elemento assorbente ed è zero, perché qualsiasi numero moltiplicato per zero dà come risultato zero.
$$ 7 \times 0 = 0 $$
Se ti ricordi queste semplici regole, puoi affrontare qualsiasi moltiplicazione.
Un consiglio. Conoscere le tabelline facilita enormemente i calcoli moltiplicativi. Ecco la tabellina del 1 al 10:
| Moltiplicatore | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Quindi, prima di affrontare qualsiasi cosa più complicata, devi passare per il girone delle tabelline. Se non le conosci o le hai dimenticate, ripassale!
Moltiplicazione di numeri a più cifre
E adesso la parte divertente: moltiplicare numeri più grandi. Esistono diversi metodi ma i principali sono i seguenti:
Metodo della moltiplicazione in colonna
Ad esempio, calcola la moltiplicazione 23 × 45
1] Scrittura dei numeri in colonna
Prima di tutto, scrivi i due numeri uno sotto l'altro, allineando le cifre in colonna:
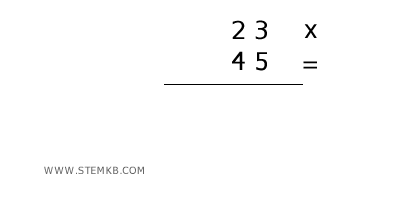
2] Moltiplica la cifra delle unità del secondo numero
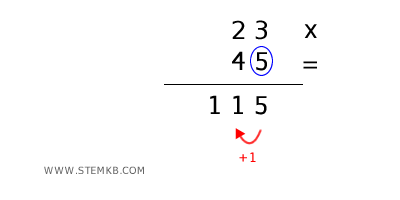
Inizia moltiplicando la cifra più a destra (5) del numero inferiore per ciascuna cifra del numero superiore (prima 3 e poi 2):
- 5×3 = 15 scrivi 5 e riporto 1
- 5×2 = 10 +1 = 11
Il primo risultato parziale è quindi 115.
3] Moltiplica la cifra delle decine del secondo numero
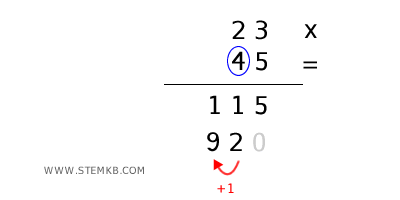
Ora, moltiplica la cifra successiva del numero inferiore (4) per le cifre del numero superiore. Ricorda che il 4 rappresenta 40, quindi devi aggiungere uno zero alla fine del risultato:
- 4×3=12 scrivi 2 e riporti 1
- 4×2=8+1=9
Il secondo risultato parziale è quindi 920.
4] Somma i risultati parziali
Infine, somma i due risultati parziali per ottenere il prodotto finale:
$$ 115 + 920 = 1035 $$
Pertanto, il prodotto finale è 23 × 45 = 1.035
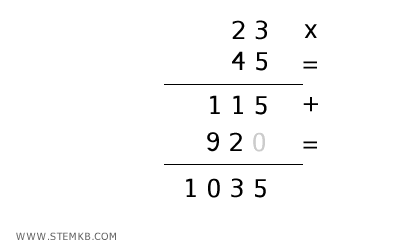
Questo metodo ti permette di eseguire moltiplicazioni a più cifre in modo chiaro e organizzato, seguendo un processo passo dopo passo.
Moltiplicazione con decimali
Quando devi moltiplicare numeri decimali:
- Ignora la virgola e moltiplica come se fossero interi.
- Conta le cifre decimali (n) in entrambi i numeri.
- Rimetti la virgola nel risultato finale dopo n posizioni a partire da destra
Ad esempio, prova a moltiplicare questi numeri $ 2,5 \times 0,4 $
- Togli la virgola e moltiplica i numeri come se fossero interi $$ 25 \times 4 = 100 $$
- Conta le cifre decimali nei due numeri: 1 (in 2,5) + 1 (in 0,4) = 2
- Quindi, posiziona la virgola nel numero 100 dopo due posizioni a partire da destra. Il risultato è 1,00
Il risultato finale della moltiplicazione è $ 2,5 \times 0,4 = 1,0 $
Moltiplicazione di frazioni
Prendi i numeratori e i denominatori, moltiplicali tra loro e prega che ti sia facile semplificarli.
Ad esempio:
$$ \frac{2}{3} \times \frac{4}{5} $$
$$ \frac{2 \times 4 }{3 \times 5} $$
$$ \frac{8}{15} $$
La regola del segno
La regola dei segni nella moltiplicazione stabilisce che il prodotto di due numeri è positivo se i segni dei numeri sono uguali (entrambi positivi o entrambi negativi) e negativo se i segni sono diversi.
Ad esempio, se hai due fattori positivi, il prodotto è sicuramente positivo. Il segno non cambia.
$$ 3 \cdot 4 = 12 $$
Se un fattore è positivo e l'altro è negativo, il segno negativo prevale, rendendo il risultato negativo. Il segno si inverte.
$$ 3 \cdot (-4) = -12 $$
Infine, se i fattori sono entrambi negativi, il segno è positivo. Il segno si inverte "due volte"!
$$ (-3) \cdot (-4) = 12 $$
Quest'ultima regola è poco intuitiva ma puoi vederla come una "doppia inversione": il primo segno negativo inverte il segno iniziale, e il secondo lo riporta al positivo.
Ad esempio, immagina \( -3 \) come \( 3 \cdot (-1) \), cioè il numero positivo \( 3 \) moltiplicato per \( -1 \), che cambia il segno da positivo a negativo. Ora, calcola $$ (-3) \cdot (-4) = 3 \cdot (-1) \cdot (-4) $$ Il primo passaggio, \( 3 \cdot (-1) \), ti dà \( -3 \). Poi, moltiplicando questo risultato per \( -4 \), hai una "seconda inversione" che porta il segno da negativo a positivo: $$ -3 \cdot (-4) = +12 $$ In sostanza, il segno cambia due volte, portando il risultato finale a essere positivo.
In sintesi, due segni uguali danno un risultato positivo, due segni diversi danno un risultato negativo.
La moltiplicazione è un'operazione interna ai numeri naturali
Quando moltiplichi due numeri naturali tra loro, il prodotto è sempre un altro numero naturale.
Ad esempio, moltiplica i numeri 4 e 2.
$$ 4 \times 2 = 8 $$
Il risultato è 8 che è un altro numero naturale.
Per indicare questa proprietà diciamo che "la moltiplicazione è un'operazione interna ai numeri naturali" e "l'insieme dei numeri naturali $ \mathbb{N} $ è chiuso rispetto alla moltiplicazione".
In generale, la moltiplicazione è un'operazione interna anche nell'insieme dei numeri interi, razionali o reali.
Il simbolo del punto
Per indicare la moltiplicazione puoi usare il simbolo "$ \times $" oppure il punto centrato "$ \cdot $"
Tecnicamente, entrambi i simboli sono utilizzati per rappresentare la moltiplicazione, ma dipende dal contesto:
- Simbolo della "×" (per). Questo simbolo è più comune nei libri di scuola elementare e nei testi più semplici, dove si vuole chiaramente indicare l'operazione di moltiplicazione. È molto visibile e facilmente riconoscibile, specialmente nei primi approcci alla matematica. Esempio: \( 4 \times 3 = 12 \)
- Simbolo del "·" (punto centrato). Questo simbolo viene usato più frequentemente in contesti matematici avanzati, come l'algebra e la fisica, per evitare confusione con la variabile "x". È preferito in scritti formali, dove "x" potrebbe essere utilizzata per rappresentare una variabile. Esempio: \( 4 \cdot 3 = 12 \)
In algebra e in molte discipline matematiche avanzate, quando due variabili o numeri sono scritti uno accanto all'altro senza segno (ad esempio, \( ab \)), si sottintende che debbano essere moltiplicati.
$$ a \cdot b = ab $$
Ora sai tutto ciò che c'è da sapere sulla moltiplicazione.

